5．质量为40 kg的物体，在光滑的水平面上做匀速直线运动，在5 s内通过的距离为10 m，那么外力对物体做的功为_____J，功率是_____W。

4．如图1所示，重为100 N的物体在F的作用下以12 m/s的速度在水平地面上做匀速直线运动，此时，弹簧秤的示数为4 N，则拉力F=_____，功率是_____W。

　　　　　　　　　　　　　　　　　　　　　　　　　　　 图1

3．举重运动员在3 s内把1500 N的杠铃举高到1.8 m，他对杠铃做了_____J的功，功率是_____W，若举在空中停了3 s，则这个过程做了_____J的功，功率是_____W。

2．两台机器的功率之比为3∶2，它们做同样的功所需要的时间之比为______；在相同的时间里，做功之比为______。

1．物体在_________叫功率，它是反应物体_____的物理量，国际单位制中的单位是_____。某机器的功率为5 W，其物理意义是_________。

1．人用筐将砖运送到楼上。2．人用滑轮将砖运送到楼上。3．使用起重机将砖运送到楼上。

提问：以上三种方法，除了机械效率不同外还有什么不同。(待学生思考不必要求立即回答)。 [例2] 一个人用通常的步伐走上三楼，或以快速地跑到三楼上。

提问：两种方法所做的功的情况有何不同。(要求同上题，先认真去思考，不必急于作答。) [例3] 有一个重型的机器，需要推至距100米远的厂房内。

方法有三： 　1．工人们用推力推到厂房内。 　2．工人们用车推到厂房内。 3．用马车拉到厂房内。

提问：三种方法完成此功有何不同。

对比上述三例，当人们完成一定的功时，存在着一个具体的实际问题是什么？

启发同学得出答案： 物体做功有快、有慢。

在例1中起重机做功快。 例2中人跑到三楼做功快。 例3中用马车做功快。

物理学里用功率来表示物体做功的快慢，板书：因此，单位时间里完成的功，叫做功率。

根据定义可得出：

板书：各物理量的国际单位，写在公式中。

1瓦特＝1焦耳/秒，1千瓦＝1000瓦，1兆瓦＝106瓦特。

指出：功率是机器的主要技术性能之一。

功率小，做功慢，耗能少。 　　　功率大，做功快，耗能多。

[例题] 高出水面30米处有一个容积是50米3的蓄水池，要用一台离心式水泵抽水给蓄水池，1小时能把水池充满即可，这台水泵的功率至少是多少千瓦？

已知：h＝30米，V＝50米3，

t＝1小时＝3600秒，

求：P

解：分析，根据已知条件

m＝ρV。

m＝1×103千克/米3×50米3＝5×104千克

所以G＝5×105牛顿。

W＝Gh ＝5×105牛顿×30米＝15×106焦耳。

答：这台水泵的功率至少是4.2千瓦。

指出：根据已知条件和所求的物理量的基本公式，知道水泵是克服水重而做功，故在题内首先根据水的质量求出水重，这样再代入功率的基本公式中求功率。

为什么题目最后所求的是“功率至少是”多少千瓦？为什么不求等于多少或者求最大是多少千瓦。

这是因为在实际中水泵有轴功率和配套功率的区别，轴功率是指单独水泵本身所能完成的功率，如果按题内所求功率，只能满足轴功率，那么水泵是无法工作的，因为水泵必须同其它机器配合使用才能工作，所以配套功率是要大于轴功率的，这是否是功率越大越好呢？不是的，因为功率越大，必定耗电或耗油多，是不符合经济效益的。

作业习题1、2、3。

[习题演练]

3．提高机械效率的主要办法是：改进机械的结构，例如提水时用容积较大而重量较轻的水桶，按规程进行保养、合理使用以减小摩擦．

2．略

1．起重机做的有用功是

W_有用=Gh=3600 N×4 m=14400 J

总功为有用功和额外功之和

W_总=W_有用+W_额外=14400 J+9600 J=24000 J

其机械效率为

η===60%

起重机提升装货物用的容器所做的功、各部件之间的摩擦做功等都是额外功．

2．机械效率

在实际做功的过程中，虽然不得不做一些额外功，但我们总是希望额外功能小一些，可以减小不必要的能量的损耗．这样一来，有用功在总功中占的比例就会大些．为了表示这个比例，物理学中引入了机械效率这个物理量．

(1)定义和定义式

机械效率被定义为：有用功与总功的比值，用希腊字母“η”表示．

根据定义写出公式：η=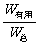

(2)说明

关于机械效率，在此我要做两点说明：

一是在实际计算中，机械效率通常被表示为一个百分数；

二是由于W_总＞W_有用，所以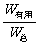＜1，因此机械效率必然小于100%．如果有人告诉你某机器：η大于1或大于100%，那肯定是错误的．

(3)简单计算

将功的计算公式与机械效率的计算关系相结合，我们来做一个例题：

例：起重机把质量为0.6 t的重物提升了3 m，而它的电动机所做的功是3.4×10⁴ J，起重机的机械效率是多少？

解：起重机提升重物所做的功为有用功，因此：

W_有用=Fh=(　　 )=mgh

=0.6×(　　 ) kg×(　　 )×3 m =1.8×10⁴ J

W_总=3.4×10⁴ J

所以η=(　　 )= =(　　 )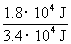

计算时要注意结果为百分数．

(4)斜面的机械效率

在这里，我们来探究一下斜面的机械效率．

在影响机械效率的许多因素中，摩擦是一个重要因素．例如，把物体拉上斜面时，就要克服物体与斜面之间的摩擦力而做额外功，这里我们要研究的是：光滑程度一样的斜面，当它的倾斜程度不同时，斜面的机械效率是否相同．

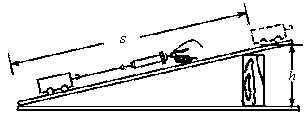如图14-14所示，找一条长木板，一端垫高，成为一个斜面．我们的目的是把物体抬到高度为h的位置．因此，我们无论采

用什么方法，都要达到这个目的，所

以我们所做的有用功就是相当于直接

把重力为G的物体抬高h时所做的功，

所以W_有用=Gh．

　　　　　　　　　　　　　　　　 图14-14

为了省力，我们往往不把重物竖直提升，而是采用一些省力的机械，斜面就是省力机械，因此，我们把重物放在斜面上，用力F将它拉到斜面顶部，如果斜面长为s，那么在此过程中做的总功为W_总=Fs．

由此分析可见，在实验过程中知道了G、h、F、s的大小，才能计算出W_有用和W_总，才能计算出机械效率．

把小车放在斜面上，用弹簧秤拉着小车在斜面上匀速上升，注意要让小车保持匀速直线运动，读出这时拉力F的大小，当小车达到高度h时停止，用刻度尺测出小车移动的距离s和小车被抬高的高度h，用弹簧秤测出小车的重力G，记录到下面的表格中．改变木板的倾斜程度，再测量两次斜面的机械效率．

在进行探究实验之前，你猜想一下：斜面能省力多少与斜面的倾斜程度有什么关系？斜面的机械效率与它的倾斜程度有什么关系？完成探究后再看，你当初的猜想是否正确．

[学习方法指导]

求机械效率的方法

求简单机械的机械效率是日常生活、生产中常遇到的问题．先来看两道例题：

例1：一斜面长5 m，高2 m，用500 N的力沿斜面将重为1000 N的物体推上去，求它的机械效率．

解：在此过程中总功为推力做的功：

W_总=F·s=500 N×5 m=2500 J

有用功为将物体抬到斜面顶部的功：

W_有用=F′·s′=Gh=1000 N×2 m=2000 J

则机械效率为：　　　　　　　　　 　　　　　　　　　　　　　　　　

η=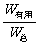==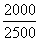80%　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

例2：如图14-15滑轮组，被提起的是质量200 g的物体，对绳子自由端的实际拉力是0.8 N，当物体升高0.2 m时，求滑轮组的机械效率．

解：有用功为

W_有用=F′·s′=G·h=mgh

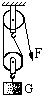=0.2 kg×10 N/kg×0.2 m

=0.4 J

动滑轮由3股绳子承担，所以

s=nh=3×0.2 m=0.6 m

则总功为

W_总=Fs=0.8 N×0.6 m=0.48 J　　　　　　　　　　　　　　　　　　　　 图14-15

η===83.3%

在这两道例题中，我们不难看出，当机械用于提高物体时，有用功为不用机械而直接将物体匀速提高做的功，即有用功为W_有用=Gh，而总功为拉力大小与物体在拉力方向移动的距离，即W_总=Fs．

在滑轮组的机械效率中，s=nh(n为共同承担动滑轮的绳子股数)，但由于考虑摩擦和滑轮的重力，F≠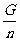，这一点你应该注意．

通过上述分析，我们可以得出计算简单机械的机械效率公式为η= =．

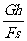你学会了吗？可以用这种方法做两道题试试．

[知识拓展]

机械效益

使用机械的最终目的之一是省力．就一般而言，不同的机械省力的情况不同．为了比较各种不同机械的省力程度，物理上还引入了一个机械效益的概念．机械效益定义为机械产生的对外作用力(P)跟外界施于机械的力(F)之比，若以A表示机械效益．则：

A=

对于杠杆，A就是动力和阻力之比；对于轮轴，在不考虑摩擦情况下，A等于轮半径和轴半径之比；对于斜面，在忽略摩擦的情况下，A等于斜面的长和高之比．根据定义，机械效益是由实际测得的机械对外作用力(有用阻力)和外界施于机械的力(动力)的大小所决定的．同样克服一个有用阻力，有时因为机械润滑得好，无用阻力就小，需要的动力也就小．因此，机械效益就大，反之，机械效益就小．新机械的机械效益往往比旧机械的机械效益　大些．

机械效益又称“机械利益”，有时亦称“力比”．概括地说，机械效益是一个描述机械省力程度的物理量．

机械效率与机械效益的联系和区别：

机械效率与机械效益是两个比较类同的概念，使用时稍不留心就要混淆．经过以上分析，我们可以得出以下两点：

(1)机械效率是描写机械做功本领程度的一个物理量，它研究机械做功情况时引出；机械效益是描述机械省力程度的一个物理量，它研究机械省力情况时引出．

(2)机械效率与机械效益都是一个无单位的纯数，机械效率η总是小于1，而机械效益A可以小于1，也可以等于1或大于1．

[问题点拨]