
练习: 如图下部分的几何体是否为棱台?为什么?(答:不是,上下底面的对应边不平行)
如图下部分的几何体是否为棱台?为什么?(答:不是,上下底面的对应边不平行)
(二)介绍棱柱、棱锥、棱台的画法
3、棱台
⑴观察棱台的模型,说明如何形成,并演示其形成过程
⑵说明棱台的相关定义
⑶类比棱台的表示方法
⑷棱台的特点:棱台的每个底面是相似的多边形,且对应边平行,侧面是梯形
练习:如图的形状是否为棱锥,说明理由: (不是:,因为侧棱不交于一点。)
(不是:,因为侧棱不交于一点。)
2、棱锥
⑴演示当棱柱的一个底面收缩为一个点时的情况,说明因为象一个锥子,所以叫棱锥。给出棱锥的定义:当棱柱的一个底面收缩为一个点时得到的几何体,叫棱锥;这个点叫做棱锥的顶点,原棱柱的底面、侧面、侧棱仍然称棱锥的底面、侧面、侧棱。
⑵对照棱柱的表示方法,总结棱锥的表示方法。
⑶通过图形比较得出棱锥的特点:底面是多边形,侧面是由一个公共点的三角形。
 记为三棱柱ABC-A1B
记为三棱柱ABC-A1B 表示为四棱柱ABCD-A1B
表示为四棱柱ABCD-A1B
⑸让学生观察总结出棱柱的特点:两个底面与平行于底面的截面是全等的多边形且对应边平行,侧面都是平行四边形
1、棱柱
⑴展示棱柱的模型及图片,汇总名称,(因其形状如柱子)故称棱柱,但不能这样定义:形状如柱子的几何体称棱柱。如何定义呢?
⑵几何画板展示棱柱的形成过程
⑶严格的棱柱相关的定义:一般地,由一个平面多边形沿某一方向平移形成地几何体称棱柱;平移起止位置的两个面叫棱柱的底面,多边形的边形成的面叫棱柱的侧面;每两个侧面的交线称棱柱侧棱。
⑷学生根据以往的经验,来表示棱柱:根据底面的形状是几边形,相应称作几棱柱,在后面加上棱柱的底面。如:
A.0.013MeV B.0.017MeV C.0.076MeV D.0.093MeV
30.若原子的某内层电子被电离形成空位,其它层的电子跃迁到该空位上时,会将多余的能量以电磁辐射的形式释放出来,此电磁辐射就是原子的特征X射线.内层空位的产生有多种机制,其中的一种称为内转换,即原子中处于激发态的核跃迁回基态时,将跃迁时释放的能量交给某一内层电子,使此内层电子电离而形成空位(被电离的电子称为内转换电子)。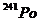 的原子核从某一激发态回到基态时,可将能量E0=1.416MeV交给内层电子(如K、L、M层电子,线K、L、M标记原子中最靠近核的三个电子层)使其电离.实验测得从241Po原子的K、L、M层电离出的电子的动能分别为Ek=1.323MeV、EL=1.399MeV、EM=1.412MeV.则可能发射的特征X射线的能量为 ( )
的原子核从某一激发态回到基态时,可将能量E0=1.416MeV交给内层电子(如K、L、M层电子,线K、L、M标记原子中最靠近核的三个电子层)使其电离.实验测得从241Po原子的K、L、M层电离出的电子的动能分别为Ek=1.323MeV、EL=1.399MeV、EM=1.412MeV.则可能发射的特征X射线的能量为 ( )
C.衰变中的质量亏损为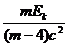
D.粒子与新核Y,的轨道半径之比为(z一2):2
B.新核Y的动能为而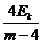
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com