解得：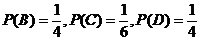

例2． 袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率为，得到黑球或黄球的概率是，得到黄球或绿球的概率也是，试求得到黑球、得到黄球、得到绿球的概率各是多少？

解：设得到红球、得到黑球、得到黄球、得到绿球依次为事件A、B、C、D，根据题意得

(3)由于“取到的两只中至少有一只正品”是事件“取到的两只都是次品”的对立事件．因而所求概率为．

(2)由于取到的2只中正品、次品各一只有两种可能：第一次取到正品，第二次取到次品；及第一次取到次品，第二次取到正品．因而所求概率为．

(1)取到的2只都是次品情况为种．因而所求概率为．?

例1．盒中有6只灯泡，其中2只次品，4只正品，有放回地从中任取两次，每次取一只，试求下列事件的概率：

(1)取到的2只都是次品；            (2)取到的2只中正品、次品各一只；?

(3)取到的2只中至少有一只正品．?

解：从6只灯泡中有放回地任取两只，共有36种不同取法．?

3、情感态度与价值观：通过数学活动，了解教学与实际生活的密切联系，感受数学知识应用于现实世界的具体情境，从而激发学习 数学的情趣。

教学重点：概率的加法公式及其应用

教学难点：事件的关系与运算

教学过程：

练习：教材P108---练习题

二、数学运用

2、过程与方法：通过事件的关系、运算与集合的关系、运算进行类比学习，培养学生的类化与归纳的数学思想。

1、知识与技能：

      （1）正确理解事件的包含、并事件、交事件、相等事件，以及互斥事件、对立事件的概念；

（2）概率的几个基本性质：

1）必然事件概率为1，不可能事件概率为0，因此0≤P(A)≤1；

2）当事件A与B互斥时，满足加法公式：P(A+B)= P(A)+ P(B)；

3）若事件A与B为对立事件，则A+B为必然事件，

所以P(A+B)= P(A)+ P(B)=1，于是有P(A)=1―P(B)

（3）正确理解和事件与积事件，以及互斥事件与对立事件的区别与联系.