
2.(常德市中考题)在使用刻度尺测量物体长度时,下列说法中正确的是( )
A.若刻度尺的零刻度线已磨损,则不能测出准确结果
B.读数时,估读的数位越多越准确
C.用多次测量求平均值的方法能减小误差
D.只要方法正确,认真测量,误差是可以避免的
1.小明发现周围同学在测长度时,刻度尺放置的位置有以下几种(图2.1-8).请你判断哪些是正确的( )

图2.1-8
6.体积的测量
(1)体积(volume):任何物体都要占据一定的立体空间,也就是具有一定的体积;
(2)体积的单位:国际单位是米3(m3).常用单位:分米3(dm3)、厘米3(cm3)、毫米3(mm3)、升(L)、毫升(mL),其换算关系如下:
1dm3=10-3m3 1cm3=10-6m3 1mm3=10-9m3
IL=ldm3 1mL=1cm3
(3)测量物体体积的方法:

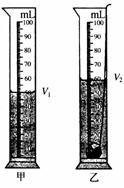
图2.1-5
说明 使用量筒或量杯测体积时,视线要与凹形水面的底相平,或与凸形水银面的顶相平.
[例4] 有一次,爱迪生把一只灯泡(还没有制成成品)交给他的助手阿普顿,让他计算出这只灯泡的容积是多少,阿普顿是普林斯顿大学数学系的毕业生,又去德国深造了一年,数学程度相当不错,他拿着这只梨形的灯泡,打量了好半天,又特地找来皮尺,上下量了尺寸,画了剖视图、立体图,还列了一道又一道的算式.一个小时过去了,爱迪生着急了,走近一看,哎哟,在阿普顿面前,好几张白纸上写满了密密麻麻的算式.爱迪生微笑着说,何必这么复杂呢?然后告诉了阿普顿测量的方法,阿普顿恍然大悟,不到一分钟就测出了灯泡的容积,你知道爱迪生测灯泡的方法吗?
思路与技巧 灯泡的形状不规则,很难直接计算出灯泡的容积.可转换成测量水的体积,即可间接地测量出灯泡的容积.
答案 爱迪生测量灯泡的容积方法是:把水装满在这只灯泡里,再把水倒在量杯或量筒里量出水的体积,则水的体积就是灯泡的容积.
探究体验
收集资料 图2.1-6是长度阶梯的一部分.请查阅相关资料将其余部分补上.并把原子、分子、人的身高、珠穆朗玛峰的高度、地球的直径、月球距离等相关的典型尺度标记在线旁(I·y=9.46×1015m).

图2.1-6
分析与结论 和其他同学交流讨论一下,还有哪些表示长度阶梯的方法?
探究点拨 用不同的方法进行物理量比较是科学方法的体现,不同的内容应选择最直观的方法.
聊天室
话题:有趣的人体尺度
胖胖:老师,公安员和考古学家能根据脚印的长度确定一个人的身高,是不是人的脚印长度与身高存在某种关系呢?
老师:人体各部分的尺度间有着特殊的规律.一般情况下,一个人手腕的周长恰恰是他脖子周长的一半。两臂平伸的长度正好等于身高,大腿正面厚度和他的脸宽差不多,肩膀最宽处约等于身高的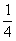 ,成年人的身高大约等于头长的8倍或7.5倍.拳头的周长与脚底的长很接近,所以买袜子的时候只要把袜底在自己拳头上绕一下,就知道是否合适了.
,成年人的身高大约等于头长的8倍或7.5倍.拳头的周长与脚底的长很接近,所以买袜子的时候只要把袜底在自己拳头上绕一下,就知道是否合适了.
用尺去量一下,你还能一发现什么规律?然后请教美术老师,画人体时应注意什么问题?

图2.1-7
快乐套餐

5.误差
(1)误差的概念:测量值与被测物体的真实值总会有些差异,这种差异叫误差;
(2)产生误差的原因:测量工具不够准确、测量方法不够完善、测量者的观察不够细致等;
(3)减小误差的方法:多次测量取平均值;
(4)误差和错误的区别:错误是测量方法或原理不正确、违反操作规则等原因造成的,是可以避免的.任何测量中的误差是不可避免的,只能选用更精密的测量工具,改进测量方法,认真细心地进行多次测量取平均值才能尽量地减小.
[例3] 小明在测量一木块长度的实验中,得到如下记录:l1=12.41cm,l2=12.42cm,l3=12.44cm,则木块的长度应为 ,小明所用刻度尺的分度值为 .
思路与技巧 多次测量求平均值能减少误差,三次测量的平均值即为木块的长度.因为在记录测量值时最后一位是估计值,求平均值时最后一位也应是估计值,估计值的位数保留多了仍是估计值,并不会变得更准确,所以位数保留多了没有意义.木块长度 l= =
=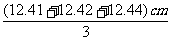 =12.423mcm=12.42cm.由于12.4cm是准确值,0.02cm是估计值,即准确到124mm,则小明所用刻度尺的分度值为1mm.
=12.423mcm=12.42cm.由于12.4cm是准确值,0.02cm是估计值,即准确到124mm,则小明所用刻度尺的分度值为1mm.
答案 12.42cm 1mm.
4.测量长度的一些特殊方法
普通方法不能直接测量出来,可以间接测量.间接测量长度的特殊方法很多,常用的有以下几种:
(1)累积法:把多个相同的微小量放在一起进行测量,再将测量结果除以被测量的个数,得出被测量值.例如:测纸张的厚度、邮票的厚度、硬币的厚度、头发的直径、细铜丝的直径等;
(2)替代法:测量某个与被测量相等的量,用以代替对被测量的直接测量.例如:测量地图上某条大河的长度、铁路的长度、海岸线的长度等.可以用一根弹性不大的柔软丝线与地图上的曲线重合,并在两端点做好记号,然后将丝线拉直,用刻度尺测出两个记号间的距离即可;
(3)平移法:当物体的长度不能直接测量时(如球的直径,圆锥体的高等),就要想办法把它等值平移到物体的外部,再用刻度尺测量.图2.1-3就是平移法在测量硬币直径时的两种应用;
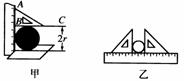
图2.1-3
(4)滚动法:先测出某个轮子的周长,让此轮子在被测曲线上滚动,记录滚动的圈数.然后用轮子周长乘以圈数就可得到曲线路径的长度,例如:测操场的长度、两个汽车站间的距离等.汽车的计程器就是根据这个原理制成的.
[例2] 现有一个圆柱形封闭油桶,仅有一个钢卷尺(量程满足测量要求)、一支粉笔和一个重锤线,不许通过计算,不许打开油桶,要求直接测量出封闭油桶的上、下边缘上两点间的最大直线距离.请设计一个试验方案,说明具体方法.
思路与技巧 封闭油桶的上、下边缘上两点间的最大直线距离在油桶内部,但题中要求不许通过计算,不许打开油桶,因此必须把这一待测的距离想办法由桶内平移到桶外,这样就可以用卷尺直接量出它的长度了.
答案 具体方法:(1)油桶直立在水平地面上,用粉笔在地上沿桶底画一个圆
(2)将油桶平移至与圆相切的位置,设切点为P(如图2.1-4)

图2.1-4
(3)利用重垂线找出切点P正上方桶边缘上的点Q
(4)用卷尺找出过P点的圆的直径,确定直径另一点M的位置
(5)利用卷尺直接量出M、Q两点间的距离即为所求.
3.正确使用刻度尺的方法
一看:测量前根据实际需要选择测量工具,并观察刻度尺的量程、分度值和零刻度线是否磨损;
二放:尺要与被测长度重合(或平行),且刻度线紧贴被测物体放置,若用零刻度线已磨损的刻度尺,应从看得清楚的某一刻度线开始量;
三读:读数时视线应与尺面垂直,并估读到分度值的下一位;
四记:记录测量结果时,要写出数字和单位.
2.长度(length)的测量
(1)常用的测量长度的工具:如图2.1-2;
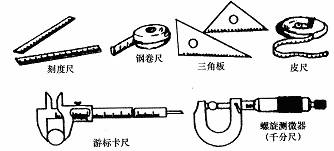
图2.1-2
(2)长度的单位:国际单位是米(meter,简写为m),常用单位有:千米(km)、分米(dm)、厘米(cm)、毫米(mm)、微米(μm)、纳米(nm).它们之间的换算关系:
1km=103m 1dm=10-1m 1cm=10-2m
1mm=10-3m 1μm=10-6m 1nm=10-9m
说明
(1)1983年国际计算大会规定:米是在 内,光在真空中行程的长度;
内,光在真空中行程的长度;
(2)光年是长度单位,用来表示天体之间的距离 。它等于光在1年中的行程.1光年=9.46×1015m.
1.物质世界的尺度,如图2.1-1
[例1] 试就你已知的物体从小到大顺序排列.
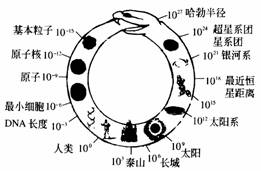
图2.1-1 物质世界的尺度/m
思路与技巧 物质从微观到宏观其尺度应分别为:夸克(小于10-16)、质子(10-13cm)、原子核(10-10cm)、原子(10-8cm)、分子(10-5-10-7cm);西瓜(60cm)、地球(1.28×106m)、太阳系、银河系(十万光年)、宇宙.
答案 夸克、质子、原子核、原子、分子、尘粒、西瓜、地球、太阳系、银河系、宇宙。
3.情感、态度与价值观 认识测量长度和体积的工具及其发展变化的过程;培养实事求是、热爱科学的精神.
探究指导
物理宫殿
2.过程与方法 经历测物体的长度和体积的过程;体验通过日常经验估测长度的方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com