
3、体验数学发展的一个重要原因是生活实际的需要,激发学生学习数学的兴趣.
2、会区分两种不同意义的量,会用符号表示正数和负数;
1、整理前两个学段学过的整数、分数(包括小数)的知识,掌握正数和负数的概念;
P 35-36 习题:2.1 2,3,7
4、 有理数的两种分类。
3、 正数与负数在形式上的区别。
2、 我们引进正负数是为了解决什么矛盾呢?
1、 数怎么不够用了呢?
.例1、(1)在知识竞赛中,如果用+10分表示加10分,那么扣20分怎么表示?
(2)某人转动转盘,如果用+5圈表示沿逆时针方向转了5圈,那么沿顺时针方向转了12圈怎样表示?
(3)在某次乒乓球质量检测中,一只乒乓球超出标准质量0.02克,记作+0.02克,那么-0.03克表示什么?(师生共同完成)
解:(1)扣20分,记作-20分;
(2)沿顺时针方向转12圈记作-12圈;
(3)-0.03克表示乒乓球的质量低于标准质量0.03克。
[在讲例1之前,先讲一下语文中有关的反义词,如:前后,上下,升降.并指出在这些词语中习惯约定
对应的是正负.讲完例1后,请几位学生出题,其它同学完成]
课堂练习2:P34 随堂练习;
练习3:P36习题2.1的第4题
做一做:
将所有学过的数进行分类,前后桌四人可进行交流。
讨论得出:]
 整数 整数 |
|
正整数:如1,2,3… 零:0 负整数:如-1,-2,-3… |
|
正分数:如 … 负分数:如 … |
|
分数 |
指出:整数和分数我们统称它们为有理数(rational number)。
想一想,还有其它的分类方法吗?
有理数还可按照性质符号来分类,分为:正有理数,负有理数,零
课堂练习:P35,习题2.1 1 P36,习题2.1 5
接下来,请同学们翻开课本P35,读一读负数小史,看看负数有怎样的历史。
上面出现了比0低的得分,我们可以用带有“-”号(读作:负)的数来表示。如:扣10分可以表示成-10分。
那么,对于比0高的得分,可以在其前面加上“+”号(读作:正),如:加10分可以写成+10分,加20分可以写成+20分。
这样,我们就可以用带有“+”号和“-”号的数表示各队每道题的得分情况。
请同学们填写下表:
投影课本P32表格。
讨论:前面出现了比0低的得分、比0高的得分,这两个量有何关系?并举例说明。
[学生得出是两个意义相反的量,教师指出像这样的两个量我们称它们为具有相反意义的量。在我们的生活中,有这样的两个量吗?让同桌同学相互举出一个例子,同桌不能判断的由教师一一讲解 ]
议一议:
在我们的生活中,有见过带有“-”号的数吗?(同桌交流)
(如:比0低的得数,零下温度,亏损额,等等)。
概括出:
像5,1.2, 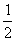 ,… 这样的数叫做正数(positive
number),它们都比0大。
,… 这样的数叫做正数(positive
number),它们都比0大。
如果要突出数的符号,可在正数前加“+”号.
在正数前面加上“-”号的数叫做负数(negntive number), 如-10,-3,…
课堂练习1、(P36,习题2.1 6)
所有的正数组成正数集合,所有的负数组成负数集合。任意写出5个正数和5个负数,并分别把它们填入所属的集合内。
正数集合:{ …};负数集合{ …};
交流讨论:有同学如果把是正数集合写成:{0,1,2,3…}对吗?
如果把负数集合写成:{-1,0,-2,-4,-6…}呢?
那么0是正数还是负数呢?
(引用“蝙蝠的故事”说明)
思考得出:
0既不是正数,也不是负数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com