(三)考点指要

　 1. 正数与负数是实际需要而产生的

　　 正数和负数是根据实际需要而产生的，随着知识面的拓宽，小学学过的自然数、分数和小数已不能满足实际需要，比如一些具有相反意义的量，收入200元和支出100元，零上6℃和零下4℃等等。它们不但意义相反，而且表示一定的数量。怎么表示它们呢？我们把一种意义规定为正的，把另一种和它意义相反的量规定为负的，这样就产生了正数和负数。

　 2. 正数和负数的概念

　　 (1)象5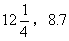，……这样的数叫正数。

　　 如等都是正数。

　　 在正数前面加上“－”(读作负)号的数叫做负数。

　　 如等都是负数。

　　 (2)零既不是正数也不是负数，它表示正数和负数的分界。

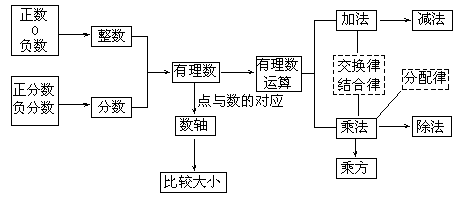
　 3. 有理数的有关概念

　　 (1)整数和分数统称为有理数。

　　 注意：整数也可以看成分母为1的分数，但为了研究方便，本章中分数就是指不包括整数的分数。

　　 (2)整数包括正整数、零、负整数。

　　 (3)分数包括正分数和负分数。

　 4. 有理数分类

　　 (1)按正数、负数和0的关系分类：

　　

　　 (2)按整数和分数的关系分类：

　　

[典型例题]

　 例1. 说明下列语句的实际意义。

　　 (1)温度上升℃

　　 (2)运进吨化肥

　　 (3)向东走了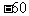米

　　 (4)盈利元

　　 解析：正确理解“－”号的意义是表示相反意义，因此上升℃，实际是下降3℃。

　　 解：(1)温度下降3℃；

　　 (2)运出200吨化肥；

　　 (3)向西走了60米；

　　 (4)亏损了15000元。

　 例2. 某人月收入1800元表示为1800元，那么每月支出350元应该怎样表示？

　 　解析：收入与支出是互为相反意义的量，收入1800元用+1800元表示，支出应用元表示。

　　 解：每月支出350元表示为元

　 例3. 把下列各数填在相应的集合内。

　　

　　 整数集合：{　　　　　　　　　　　　　　　　　　　　　 ……}

　　 负数集合：{　　　　　　　　　　　　　　　　　　　　　 ……}

　　 分数集合：{　　　　　　　　　　　　　　　　　　　　　 ……}

　　 非负数集合：{　　　　　　　　　　　　　　　　 ……}

　　 正有理数集合：{　　　　　　　　　　　　　　　　　 ……}

　　 负分数集合：{　　　　　　　　　　　　　　　　 ……}

　 　解析：(1)集合是指具有某一特征的一类事物的全体，注意不要漏掉数0，题目中只是具体的几个符合条件的数，只是一部分，所以通常要加省略号。

　　 (2)非负数表示不是负数的所有有理数，应为正数和零，那么非正数表示什么呢？(答：负数和零)

　　 答案：整数集合：{……}

　　 负数集合：{……}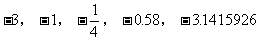

　　 分数集合：{……}

　　 非负数集合：{……}

　　 正有理数集合：{……}

　　 负分数集合：{……}

　 例4. 判断题。

　　 (1)一个数不是正数就是负数。(　　 )

　　 (2)海拔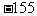米表示比海平面低155米。(　　 )

　　 (3)温度0℃就是没有温度。(　　 )

　　 (4)零是最小的有理数。(　　 )

　　 (5)零是正数。(　　 )

　　 解析：本题能很好的考查对概念的掌握。

　　 解：(1)×；(2)√；(3)×；(4)×；(5)×

[模拟试题](答题时间：30分钟)

［基础测试］

　 1. 将下列各数填入相应的集合里。

　　

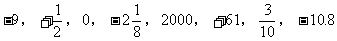
　　 正数集合：{　　　　　　　　　　　　　　　　　 ……}

　　 负分数集合：{　　　　　　　　　　　　 ……}

　　 非负数集合：{　　　　　　　　　　　　 ……}

　　 整数集合：{　　　　　　　　　　　　　　　　　 ……}

　 2. 用正数和负数表示下列各量：

　　 (1)零上24℃表示为_________，零下3.5℃表示为__________。

　　 (2)足球比赛，赢2球可记作_________球，输1球可记作_________球。

　　 (3)如果自行车链条的长度比标准长度长2mm，记作+2mm，那么比标准长度短1.5mm，记作_________mm。

　 3. 判断：

　　 (1)正整数集合和负整数集合统称整数集合。(　　 )

　　 (2)正数集合和负数集合合并在一起是有理数集合。(　　 )

　　 (3)运出20吨货物记作，则运进25吨货物记作+25。(　　 )

　　 (4)如果下降记作“－”，则不升不降记作0。(　　 )

［迁移与探究］

　 4. 下列结论中一定正确的是(　　 )

　　 A. 若一个数是整数，则这个数一定是有理数

　　 B. 若一个数是有理数，则这个数一定是整数

　　 C. 若一个数是有理数，则这个数一定是负数

　　 D. 若一个数是有理数，则这个数一定是正数

　 5. 下列说法中，正确的是(　　 )

　　 A. 有最大的负数，没有最小的正数

　　 B. 没有最大的有理数，也没有最小的有理数

　　 C. 有最大的非负数，没有最小的非负数

　　 D. 有最小的负数，没有最大正数

　 6. 关于“零”的说法正确的是(　　 )

　　 (1)是整数，也是有理数；

　　 (2)不是正数，也不是负数；

　　 (3)不是整数，是有理数；

　　 (4)是整数，不是自然数。

　　 A. (1)(4)　　　　　　　　　　 B. (2)(3)

　　 C. (1)(2)　　　　　　　　　　 D. (1)(3)

　 7. 教室高2.8米，课桌高0.6米，如果把课桌面记作0米，则教室的顶部和地面分别记作什么？教室中天花板与地面的距离是多少？如果以天花板为0米，那么桌面高度和地面各记作什么？

(二)本章知识框图

　　

(一)同学们好，从本章开始大家进入初中阶段的数学学习，大家会学习到许多新的数学知识，在学习之前先提出几点要求，以帮助大家更好的学习。

　　 (1)上课认真听讲，记好笔记中关键性的例题和老师的解题思路。

　　 (2)每天应认真复习课上所学知识后，完成当天所留作业，对新知识做适当的预习，关注课本中的每一句话和关键语句，加以理解和记忆。

　　 (3)养成勤学好问的好习惯，多与同学老师进行交流。

　　 (4)及时订正错题，建议准备一个改错本，收集出过错的题目，理解的基础上加以记忆。

　　 最后预祝同学们都能取得优异的成绩。

(六)作业

作业本(2)第1页

(五)小结

以问题的形式，要求学生思考交流：

1、引入负数后，你是怎样认识数0的，数0的意义有哪些变化?

2、怎样用正负数表示具有相反意义的量?

(用正数表示其中一种意义的量，另一种量用负数表示；特别地，在用正负数表示向指定方向变化的量时，通常把向指定方向变化的量规定为正数，而把向指定方向的相反方向变化的量规定为负数．)

(三)巩固练习

教科书第6页练习

(二)问题解决

问题3：教科书第6页例题

说明：这是一个用正负数描述向指定方向变化情况的例子，通常向指定方向变化用正数表示；向指定方向的相反方向变化用负数表示．这种描述在实际生活中有广泛的应用，应予以重视，教学中，应让学生体验“增长”和“减少”是两种相反意义的量，要求写出“体重的增长值”和“进出口额的增长率”，就暗示着用正数来表示增长的量．

归纳：在同一个问题中，分别用正数和负数表示的量具有相反的意义(教科书第6页)．

类似的例子很多，如：

水位上升-3m，实际表示什么意思呢?

收入增加-10%，实际表示什么意思呢?

等等．

可视教学中的实际情况进行补充．

(一)知识回顾和深化

回顾：上一节课我们知道了在实际生产和生活中存在着两种相反意义的量，为了区分这两种量，我们用正数表示其中一种意义的量，那么相反意义的量就用负数来表示．

这就是说：数的范围扩大了(数有正数和负数之分)．那么，有没有一种既不是正数又不是负数的数呢?

问题l：有没有一种既不是正数又不是负数的数呢?

学生思考并讨论．

(数0既不是正数又不是负数，是正数和负数的分界，是基准．这个道理学生并不容易理解，根据学生的讨论情况作些启发和引导)

例如：在温度的表示中，零上温度和零下温度是两种相反意义的量，通常规定零上温度用正数来表示，零下温度用负数来表示。那么某一天某地的最高温度是零上7℃，最低温度是零下5℃时，就应该表示为+7℃和一5℃，这里+7℃和一5℃就分别称为正数和负数．

那么当温度是零度时，我们应该怎样表示呢?(表示为0℃)，它是正数还是负数呢?由于零度既不是零上温度也不是零下温度，所以，0既不是正数也不是负数．

问题2：引入负数后，数按照“两种相反意义的量”来分，可以分成几类?

重点：深化对正负数概念的理解．

难点：正确理解和表示向指定方向化的量．