
1.经历探索直角三角形中边角关系的过程,理解正弦和余弦的意义.
5.课时小结
备课资料
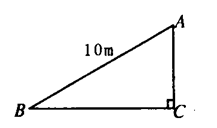 [例1](2003年浙江沼兴)若某人沿坡度i=3:4的斜坡前进10米,则他所在的位置比原来的位置升高________米.
[例1](2003年浙江沼兴)若某人沿坡度i=3:4的斜坡前进10米,则他所在的位置比原来的位置升高________米.
分析:根据题意
(如图):在Rt△ABC
中
AC:BC=3:4,
AB=10米.
设AC=3x,BC=4x,根据勾股定理,得(3x)2+(4x)2=10,
∴x=2.
∴AC=3x=6(米).
因此某人沿斜坡前进10米后,所在位置比原来的位置升高6米.
解:应填“6 m”.
 [例2](2003年内
[例2](2003年内
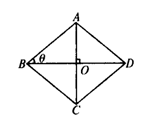
蒙古赤峰)菱形的两条
对角线分别是16和12.
较长的一条对角线与菱
形的一边的夹角为θ,
则tanθ=______.
分析:如图,菱形ABCD,BD=16,AC=12,∠ABO=θ,
在Rt△AOB中,AO=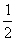 AC=6,
AC=6,
BO=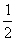 BD=8.
BD=8.
tanθ=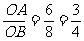 .
.
解:应填“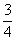 ”.
”.
4.随堂练习
3.例题讲解(略)
2.正切的定义:
在Rt△ABC中,锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫做∠A的正切,记作tanA,即
tanA= .
.
注:(1)tanA的值越大.梯子越陡.
(2)坡度通常表示斜坡的倾斜程度,是坡角的正切.坡度越大,坡面越陡.
1.当直角三角形中的锐角确定之后,它的对边与邻边之比也随之确定.
2.观察学校及附近商场的楼梯,哪个更陡.
 Ⅶ.活动与探究
Ⅶ.活动与探究
(2003年江苏盐城)
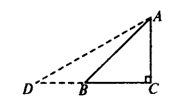
如图,Rt△ABC是一防
洪堤背水坡的横截面
图,斜坡AB的长为
12 m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改造成坡比为1:1.5的斜坡AD,求DB的长.(结果保留根号)
[过程]要求DB的长,需分别在Rt△ABC和Rt△ACD中求出BC和DC.根据题意,在Rt△ABC中,∠ABC=45°,AB=12 m,则可根据勾股定理求出BC;在Rt△ADC中,坡比为1:1.5,即tanD=1:1.5,由BC=AC,可求出CD.
[结果]根据题意,在Rt△ABC中,∠ABC=45°,所以△ABC为等腰直角三角形.设BC=AC=xm,则
x2+x2=122,
x=6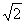 ,
,
所以BC=AC=6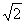 .
.
在Rt△ADC中,tanD=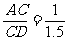 ,
,
即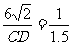 CD=9
CD=9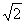 .
.
所以DB=CD-BC=9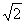 -6
-6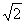 =3
=3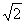 (m).
(m).
板书设计
§1.1.1 从梯子的倾斜程度谈起(一)
1.习题1.1第1、2题.
2.如图,某人从山
脚下的点A走了200m后
到达山顶的点B,已知点
B到山脚的垂直距离为55
m,求山的坡度.(结果精确到0.001)
分析:由图可知,∠A是坡角,∠A的正切即tanA为山的坡度.
解:根据题意:
在Rt△ABC中,AB=200 m,BC=55 m,
AC=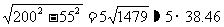 =192.30(m).
=192.30(m).
TanA=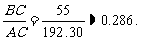
所以山的坡度为0.286.
Ⅴ.课时小结
本节课从梯子的倾斜程度谈起,经历了探索直角三角形中的边角关系,得出了在直角三角形中的锐角确定之后,它的对边与邻边之比也随之确定,并以此为基础,在“Rt△”中定义了tanA= .
.
接着,我们研究了梯子的倾斜程度,工程中的问题坡度与正切的关系,了解了正切在
现实生活中是一个具有实际意义的一个很重要的概念.
Ⅵ.课后作业
1.如图,△ABC
是等腰直角三角形,
你能根据图中所给
数据求出tanC吗?
分析:要求tanC.需从图中找到∠C所在的直角三角形,因为BD⊥AC,所以∠C在Rt△BDC中.然后求出∠C的对边与邻边的比,即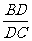 的值.
的值.
解:∵△ABC是等腰直角三角形,BD⊥AC,
∴CD=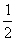 AC=
AC=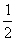 ×3=1.5.
×3=1.5.
 在Rt△BDC中,tanC=
在Rt△BDC中,tanC=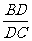 =
=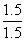 =1.
=1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com