1.如图1-11，在Rt△ABC中，∠C = 90°, BE平分∠ABC，交AC于E，DE是斜边AB的垂直平分线，若DE = 1cm，则AC = 　　　　　；.

如图1-9，C是线段AB上的一点，在AB的同侧作等边

△ACD和等边△CBE.　 F、G分别是AE、BD的中点.

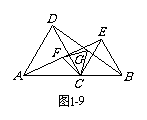求证：△CFG是等边三角形.

[综合练习]

如图1-10，已知A、D两点分别是正△DEF、正△ABC的中心,连接AD，延长AD交BC于M, 延长DA交EF于N..G是DF与AB的交点，H是DE与AC的交点，连接GH. 请写出三个不同类型的、须经过两步推理才能得到的正确结论，并给出证明.

[探究练习]

设P为等边△ABC所在平面上的一点，试找出使△PAB 、△PBC、△PCA

均为等腰三角形的所有符合条件的点P..

练习二

[基础练习] 一、1. 3； 2. 60°. 二、1. C；2. D. 三、提示：先证△ACE ≌△DCB, 再证

△ACF ≌△BCG.

[综合练习]∠GAM = 30°；DF∥AC；MN⊥GH；四边形AGDH是菱形；△AGH是等边三角形；△AGD是等腰三角形；△ABM是直角三角形；△ABC ≌△DEF；△AGH ∽△DEF；GH = ；这是一个轴对称图形；；这是一个中心对称图形 ……

[探究练习]符合条件的点P共有10个.

2.如图1-8，△PAB与△PDC是两个全等的等边三角形，且

PA⊥PD, 有下列四个结论：①∠PBC = 15°；② AD∥BC；

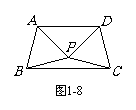③ 直线PC与AB垂直；④ 四边形ABCD是轴对称图形.

其中正确结论的个数是(　　 ).

A. 1个　　　　　　　　　　 B. 2个

C. 3个　　　　　　　　　　 D. 4个

1.如图1-7，△ABC中，AB = AC,　 AD = AE, ∠BAD = 30°, 则

∠EDC的度数为(　　　 )；

A. 10°　　　　　　　　　　 B. 12.5°

C. 15°　　　　　　　　　　 D. 18°

1. 你能证明它们吗

　　　　　 练习一

[基础练习] 一、1. BD = CE(或∠BAD =∠CAE或∠ADB =∠AEC等)； 2. 68°. 二、1. B； 2. C.　 三、1.提示：连接AC； 2. 提示：证△DBE ≌△DCF.

[综合练习] 根据题意画出图形，写出已知，求证，在进行证明

2.已知：如图1-5，在△ABC中，D是BC边的中点，DE⊥AB,

DF⊥AC, 垂足分别为E、F，且DE = DF . 求证：AB = AC.

[综合练习]

　 求证：有两条角平分线相等的三角形是等腰三角形.

1.已知：如图1-4，四边形ABCD中，AB = CB, ∠A =∠C.

求证：AD = CD.

2.将两个全等的有一个锐角为30°的直角三角形拼成如图1-3所示的图形，其中两条长直角边在同一条直线上，则

图中等腰三角形的个数是(　　　 ).

　 A. 1个　　　　　　　　　 B. 2个

　 C. 3个　　　　　　　　　 D. 4个

1.等腰三角形的底边长为5cm，一腰上的中线把周长分成两部分的差为3cm，则腰长为(　　　 )；

A. 2cm　　　　　　　　 　 B. 8cm

C. 2cm或8cm　　　　　 　 D. 7cm

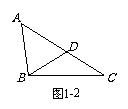
2.如图1-2，△ABC中， D为AC上一点，且AB = AD,　 DB

= DC, 若∠C = 28°,则∠A = 　　　　度.