
1.1、你能证明它们吗(一)
|
课 题 |
1.1、你能证明它们吗(一) |
课型 |
新授课 |
|
|
教学目标 |
1、了解作为证明基础的几条公理的内容,掌握证明的基本步骤和书写格式。 2、经历“探索-发现-猜想-证明”的过程。能够用综合法证明等腰三角形的关性质定理和判定定理。 |
|||
|
教学重点 |
了解作为证明基础的几条公理的内容,掌握证明的基本步骤和书写格式。 |
|||
|
教学难点 |
能够用综合法证明等腰三角形的关性质定理和判定定理。 |
|||
|
教学方法 |
观察法 |
|||
|
教学后记 |
|
|||
|
教 学 内 容 及 过 程 |
学生活动 |
|||
|
一、复习: 1、什么是等腰三角形? 2、你会画一个等腰三角形吗?并把你画的等腰三角形栽剪下来。 3、试用折纸的办法回忆等腰三角形有哪些性质? 二、新课讲解: 在《证明(一)》一章中,我们已经证明了有关平行线的一些结论,运用下面的公理和已经证明的定理,我们还可以证明有关三角形的一些结论。 同学们和我一起来回忆上学期学过的公理 w 本套教材选用如下命题作为公理 : w 1.两直线被第三条直线所截,如果同位角相等,那么这两条直线平行; w 2.两条平行线被第三条直线所截,同位角相等; w 3.两边夹角对应相等的两个三角形全等; (SAS) w 4.两角及其夹边对应相等的两个三角形全等; (ASA) w 5.三边对应相等的两个三角形全等; (SSS) w 6.全等三角形的对应边相等,对应角相等. 由公理5、3、4、6可容易证明下面的推论: 推论 两角及其中一角的对边对应相等的两个三角形全等。(AAS) 证明过程: 已知:∠A=∠D,∠B=∠E,BC=EF 求证:△ABC≌△DEF 证明:∵∠A=∠D,∠B=∠E(已知) ∵∠A+∠B+∠C=180°,∠D+∠E+∠F=180°(三角形内角和等于180°) ∠C=180°-(∠A+∠B) ∠F=180°-(∠D+∠E) ∠C=∠F(等量代换) BC=EF(已知) △ABC≌△DEF(ASA) 这个推论虽然简单,但也应让学生进行证明,以熟悉的基本要求和步骤,为下面的推理证明做准备。 三、议一议: (1)还记得我们探索过的等腰三角形的性质吗? (2)你能利用已有的公理和定理证明这些结论吗? 等腰三角形(包括等边三角形)的性质学生已经探索过,这里先让学生尽可能回忆出来,然后再考虑哪些能够立即证明。 定理:等腰三角形的两个底角相等。 这一定理可以简单叙述为:等边对等角。 已知:如图,在ABC中,AB=AC。 求证:∠B=∠C 证明:取BC的中点D,连接AD。 ∵AB=AC,BD=CD,AD=AD, ∴△ABC△≌△ACD (SSS) ∴∠B=∠C (全等三角形的对应边角相等)  四、想一想: 四、想一想: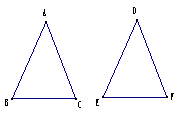 在上图中,线段AD还具有怎样的性质?为什么?由此你能得到什么结论? 在上图中,线段AD还具有怎样的性质?为什么?由此你能得到什么结论?应让学生回顾前面的证明过程,思考线段AD具有的性质和特征,从而得到结论,这一结合通常简述为“三线合一”。 推论 等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。 五、随堂练习: 做教科书第4页第1,2题。 六、课堂小结: 通过本课的学习我们了解了作为基础的几条公理的内容,掌握证明的基本步骤和书写格式。经历“探索-发现-猜想-证明”的过程。能够用综合法证明等腰三角形的关性质定理和判定定理。探体会了反证法的含义。 七、课外作业: 教科书第5页第1,2题。 板书设计:
|
这个推论虽然简单,但也应让学生进行证明,以熟悉的基本要求和步骤,为下面的推理证明做准备。 学生充分讨论问题1,借助等腰三角形纸片回忆有关性质 让学生尽可能回忆出来,然后再考虑哪些能够立即证明 让同学们通过探索、合作交流找出其他的证明方法 学生回顾前面的证明过程,思考线段AD具有的性质和特征,讨论图中存在的相等的线段和相等的角,发现等腰三角形性质定理的推论,从而得到结论,这一结合通常简述为“三线合一”。 |
|||
23.你以前证过的结论,有的是否可以用反证法证明,试试看.
22.如图5,在△ABC中,AB=AC,D是AB上一点,DE⊥BC,E是垂足,ED的延长线交CA的延长线于点F,求证:AD=AF.

图5
21.如图4,AB=CD,AD=BC,EF经过AC的中点O,分别交AB和CD于E、F,求证:OE=OF.
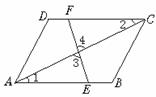
图4
20.如图3,在AB=AC的△ABC中,D点在AC边上,使BD=BC,E点在AB边上,使AD=DE=EB,求∠EDB.

图3
19.在直角三角形中,一条边长为a,另一条边长为2a,那么它的三个内角的比为( )
A.1∶2∶3 B.2∶2∶1
C.1∶1∶2 D.以上都不对
18.在△ABC中∠A∶∠B∶∠C=1∶2∶3,CD⊥AB于D点,AB=a,则BD的长为( )
A.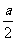 B.
B.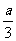 C.
C. D.以上都不对
D.以上都不对
17.△ABC中, AB=AC, CD是△ABC的角平分线, 延长BA到E使DE=DC, 连结EC, 若 ∠E =51°,则∠B等于( )
A.60° B.52° C.51° D.78°
16.如果三角形一边的中线和这边上的高重合,则这个三角形是( )
A.等边三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
15.若三角形的一边等于另一边的一半,那么这边所对的角度为( )
A.30° B.45° C.60° D.无法确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com