
1.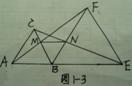 如图1-3,△ABC、△BEF都是等边三角形,AF交BC于M,CE交BF于N,
如图1-3,△ABC、△BEF都是等边三角形,AF交BC于M,CE交BF于N,
求证:①AF=CE;
②△MBN是等边三角形.
图1-3
2. 解答题:
解答题:
如图1-2,∠BAC=30°,D为角平分线上一点,DE⊥AC于F,
DF∥AC且交AB于F,若DF=10cm,
①求证:△AFD为等腰三角形;
②求DE的长. 图1-2
练习二
练习一
1. 填空题:
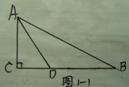
⑴如图1-1,△ABC中,∠C=90°,AD平分∠BAC, AD=BD,
CD=2cm,则∠ADC=________; AD=_______. 图1-1
⑵若△ABC的中线AD=BC,则∠A=______.
等边三角形是特殊的等腰三角形,判断某个三角形是等边三角形时,一般先证明此三角形是等腰三角形,再求得一个角为60°即可. 遇到含30°角的直角三角形,联想到“直角三角形中,30°角所对的边等于斜边的一半”.常常在直角三角形中求边长时用到,但必须注意前提是直角三角形.
学会等边三角形判定定理的证明;掌握直角三角形中,30°角所对的直角边与斜边的关系.
6. 布置作业
⑴课本习题1.3;
⑵课下思考题:
在任意三角形中,“有一个角为30°,那么它所对的边等于另一条边的一半”这个结论成立吗?
学 案
5. 课堂小结
这节课你学会了哪些内容?有何收获?
4. 随堂练习
补充题:在Rt△ABC中,∠C=90°,如果∠B=2∠A,那么∠B和∠A各是多少度?边AB与BC之间有什么关系?
|
1. 创设问题情境 ⑴一个等腰三角形满足什么条件时,便成为等边三角形? ⑵你能证明你的结论吗? ⑶从探索到证明你能否归纳出判断某个三角形是等边三角形的正确结论? 2. 新知探究 ⑴实物演示(投影)
⑵探索问题 ①上述图1-1和图1-2能否判定为等边三角形? ②你能证明你的结论吗?把你的证明思路与同伴进行交流. ⑶归纳 定理:有一个角是60°的等腰三角形是等边三角形. ⑷知识巩固 证明:三个角都相等的三角形是等边三角形. ⑸自主探索 ①用你手中两个含30°角的三角尺,你能拼成一个怎样的三角形?并说明理由. ②由此你能想到,在直角三角形中,30°角所对的直角边与斜边有怎样的大小关系?并证明你的结论. ⑹投影示范
⑺归纳 定理:在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半. 3. 应用举例 例2,等腰三角形的底角为15°,腰长为2a, 求:腰上的高. 引导学生从问题出发,根据操作实验的结果,运用归纳,类比的方法得出猜想,然后再进行证明. 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |