
1. 选择题:
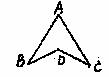
(1)如图1-6,AB=AC,AD=BD=BC,则图中共有相等的角( )
A、3对 B、6对 C、2对 D、以上都不对 图1-6
 (2)在△ABC中,∠A:∠B:∠C=2:1:1,则△ABC是(
)
(2)在△ABC中,∠A:∠B:∠C=2:1:1,则△ABC是(
)
A、等边三角形 B、锐角三角形
C、直角三角形 D、等腰直角三角形
2. 证明题:
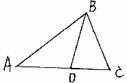
(1)如图1-3,直线EF截∠MAN的两边于B,C,且AB=AC.
求证:∠1=∠2.
图1-3
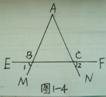
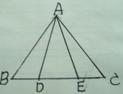 (2)如图1-4,点D、E在△ABC的边BC上,AB=AC,AD=AE.
(2)如图1-4,点D、E在△ABC的边BC上,AB=AC,AD=AE.
求证:∠BAD=∠EAC.
图1-5
图1-4
练 习 二
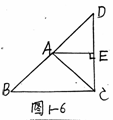
如图1-5,在△ABC中,AB=AC,延长BA至D,
使AD=AB,连结CD,AE是△ACD的高.
(1)求证:AE∥BC;
(2)当∠BAC=70°时,求∠CAE的度数.
图1-5
 练 习 一
练 习 一
1. 填空题:
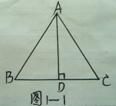
⑴如图1-1,在△ABC中,AB=AC,AD是高.
①若∠B=65°,则∠BAD=________.
②若BC=8cm, 则BD=______cm.
③若△ABC的周长为36cm,AD=10cm, 图1-1
 则△ABD的周长为_________.
则△ABD的周长为_________.
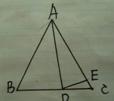
⑵如图1-2,AB=AC,AD=AE,∠BAD=28°
则∠EDC=___________.
图1-2
等腰三角形是一种特殊的三角形,遇到解决有关等腰三角形的问题时,一般是过等腰三角形的顶点作底边上的高或底边上的中线或顶角的角平分线,利用等腰三角形中的三线合一的性质.若在同一个三角形中证明两个角相等,一般要联想到等腰三角形的性质定理--等边对等角.因此需证明两边相等,从而可得到两边所对的角相等.
经历“探索--发现--猜想--证明”的过程,学会用综合法证明等腰三角形的有关性质定理.
7. 布置作业
课本第5页习题1.1
预习课本第5页至第8页.
学 案
6.课堂小结
这节课你学会了什么?有何收获?
5. 随堂练习
⑴课本第4页练习1,2题.
⑵补充题:
如图1-2,在三角形测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,调整架身,使点A恰好在重锤线上,试问AD与BC有何位置关系?
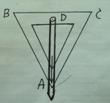
图1-2
|
教 师 活 动 |
学生活动 |
||
|
1. 提出问题 ⑴如何判定两个三角形全等? ⑵三角形全等又能得到哪些正确的结论? 2. 创设问题情境,引入新课 ⑴你还记得我们探索过的等腰三角形的性质吗? ⑵等边三角形呢? ⑶你能利用已有的公理和定理证明这些结论吗? 3. 证明等边对等角 ⑴结合上述问题(1),师生共同绘图“等腰三角形”. ⑵演示等腰三角形纸片,回忆以前的折纸过程,分析折痕将等腰三角形分成了两个全等三角形,能否通过作一条线段,得到两个全等的三角形,从而证明这两个底角相等呢? ⑶你能写出证明过程吗? ⑷演示(投影片)
(5)归纳结论 等边对等角 4. 自主探索 在图1-1中,线段AD还具有怎样的性质?为什么?由此你还能得到什么结论? 注重对证明思路的启发,提倡证明方法的多样性. 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |