2、拓展作业：《目标检测》

1、基础作业：P5页习题1.1　 1、2。

3、试用折纸的办法回忆等腰三角形有哪些性质？

新课讲解：

在《证明(一)》一章中，我们已经证明了有关平行线的一些结论，运用下面的公理和已经证明的定理，我们还可以证明有关三角形的一些结论。

同学们和我一起来回忆上学期学过的公理

w　　 本套教材选用如下命题作为公理 :

w　　 1.两直线被第三条直线所截,如果同位角相等,那么这两条直线平行;

w　　 2.两条平行线被第三条直线所截,同位角相等;

w　　 3.两边夹角对应相等的两个三角形全等; (SAS)

w　　 4.两角及其夹边对应相等的两个三角形全等; (ASA)

w　　 5.三边对应相等的两个三角形全等; (SSS)

w　　 6.全等三角形的对应边相等,对应角相等.

由公理5、3、4、6可容易证明下面的推论：

推论　两角及其中一角的对边对应相等的两个三角形全等。(AAS)

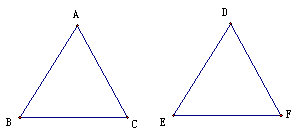证明过程：

已知：∠A=∠D,∠B=∠E,BC=EF

求证：△ABC≌△DEF

证明：∵∠A+∠B+∠C=180°，

∠D+∠E+∠F=180°

(三角形内角和等于180°)

∴∠C=180°-(∠A+∠B)

∠F=180°-(∠D+∠E)

又∵∠A=∠D,∠B=∠E(已知)

∴∠C=∠F

又∵BC=EF(已知)

∴△ABC≌△DEF(ASA)

(这个推论虽然简单，但也应让学生进行证明，以熟悉的基本要求和步骤，为下面的推理证明做准备。)

议一议：

(1)还记得我们探索过的等腰三角形的性质吗？(教师提出问题，并利用等腰三角形纸片帮议助学生回忆。学生充分讨论问题1，借助等腰三角形纸片回忆有关性质。)

(2)你能利用已有的公理和定理证明这些结论吗？

(等腰三角形(包括等边三角形)的性质学生已经探索过，这里先让学生尽可能回忆出来，然后再考虑哪些能够立即证明。)

定理：等腰三角形的两个底角相等。

这一定理可以简单叙述为：等边对等角。

已知：如图，在ABC中，AB＝AC。

求证：∠B＝∠C

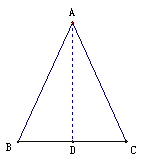(引导学生证明定理“等腰三角形的两个底角相等”，重点引导学生做辅助线，将等腰三角形分成两个全等的三角形： 我们刚才利用折叠的方法说明了这两个底角相等。实际上，折痕将等腰三角形分成了两个全等三角形。能否通过作一条线段，得到两个全等的三角形，从而证明这两个底角相等呢？)

证明：取BC的中点D，连接AD。

∵AB＝AC，BD＝CD，AD＝AD，

∴△ABC△≌△ACD　 (SSS)

∴∠B=∠C (全等三角形的对应边角相等)

(让同学们通过探索、合作交流找出其他的证明方法。做∠BAC的平分线，交BC边于D；过点A做AD⊥BC。。学生指出该定理的条件和结论，写出已知、求证，画出图形，并选择一种方法进行证明。)

想一想：

在上图中，线段AD还具有怎样的性质？为什么？由此你能得到什么结论？

(应让学生回顾前面的证明过程，思考线段AD具有的性质和特征，讨论图中存在的相等的线段和相等的角，发现等腰三角形性质定理的推论，从而得到结论，这一结合通常简述为“三线合一”。)

推论 等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。

随堂练习：

做教科书第4页第1，2题。(引导学生分析证明方法，学生动手证明，写出证明过程。)

课堂小结：

通过这节课的学习你学到了什么知识？

(学生小结：通过本课的学习我们了解了作为基础的几条公理的内容，掌握证明的基本步骤和书写格式。经历“探索－发现－猜想－证明”的过程。能够用综合法证明等腰三角形的关性质定理和判定定理。探体会了反证法的含义。)

2、你会画一个等腰三角形吗？并把你画的等腰三角形栽剪下来。

复习：

1、什么是等腰三角形？

教学难点：能够用综合法证明等腰三角形的关性质定理和判定定理(特别是证明等腰三角形性质时辅助线做法)。

3、结合实例体会反证法的含义。

2、经历“探索－发现－猜想－证明”的过程。能够用综合法证明等腰三角形的关性质定理和判定定理。

1、了解作为证明基础的几条公理的内容，掌握证明的基本步骤和书写格式。

2. 证明题(用两种方法证明)

如图1-7中，AB=AC，BD=DC.　 求证：∠B=∠C.　　　　　　　　　　　　　　　 图1-7