2、做一做：用两个含30°角的三角尺，能拼成一个怎样的三角形？能拼成一个等边三角形吗？说说你的理由。

由此你能想到，在直角三角形中，30°角所对的直角边与斜边有怎样的大小关系？能证明你的结论吗？

(提示学生根据两个三角尺拼出的图形发现结论，并证明)

证明：在△ABC中，∠ACB=90°，∠A=30°，则∠B=60°

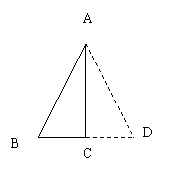延长BC至D,使CD=BC,连接 AD

∵∠ACB=90°

∴∠ACD=90°

∵AC=AC

∴△ABC≌△ADC(SSS)

∴AB=AD(全等三角形的对应边相等)

∴△ABD是等边三角形

∴BC=BD=AB

　 得到的结论：

在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

1、　 探索问题：①一个等腰三角形满足什么条件时便成为等边三角形？

　　　　　　　　　　　 ②你认为有一个角等于60°的等腰三角形是等边三角形吗？你能证明你的思路吗？(把你的思路与同伴进行交流。)

　　　　　 定理：有一个角等于60°的等腰三角形是等边三角形。

2、复习关于反证法的相关知识

练习：

证明：在一个三角形中，至少有一个内角小于或等于60°。

(笔试，进一步巩固学习证明的基本步骤和书写格式)

学一学

温故知新

1、已知：∠ABC,∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E

(1)　 找出图中的等腰三角形

(2)　 BD,CE,DE之间存在着怎样的关系？

(3)　 证明以上的结论。

2、掌握证明与等边三角形、直角三角形有关的性质定理和判定定理。

2、预习作业：P10-12页　 做一做

1、基础作业：P9页习题1.2　 1、2、3。

4、议一议1：

在上图的等腰△ABC中，如果∠ABD＝1/3∠ABC, ∠ACE＝1/3∠ACB,那么BD＝CE吗？如果∠ABD＝1/4∠ABC, ∠ACE＝1/4∠ACB呢？由此你能得到一个什么结论？

(根据图形引导学生分析归纳得出一般结论。学生分组思考、交流，在充分讨论的基础上得出一般结论写出证明过程。)

(3)　　 如果AD＝1/2AC,AE＝1/2AB, 那么BD＝CE吗？如果AD＝1/3AC,AE＝1/3AB, 呢？由此你能得到一个什么结论？

议一议2：

把“等边对等角”反过来还成立吗？你能证明？

定理证明

已知：在ΔABC中∠B=∠C

求证：AB=AC　　　　　　 (引导学生证明定理)

方法如下：

(1)

(2)

课堂小结1：

(1)　 归纳判定等腰三角形判定有几种方法,

(2)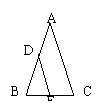证明两条线段相等的方法有哪几种。(讨论、交流)

随堂练习：

已知：在ΔABC中，AB=AC，D在AB上，DE∥AC

求证：DB=DE

(引导学生分析证明方法，学生动手证明，写出证明过程。)

想一想:

小明说，在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等,你认为这个结论成立吗?如果成立,你能证明它?

证明P₈

反证法的概念 P₈

课堂小结2：

通过这节课的学习你学到了什么知识？了解了什么证明方法？

(学生小结：掌握证明的基本步骤和书写格式。经历“探索－发现－猜想－证明”的过程。能够用综合法证明等腰三角形的两条腰上的中线(高)、两底角的平分线相等，并由特殊结论归纳出一般结论。等腰三角形的判定定理。了解反证法的推理方法。)

3、证明：

(1)　　 例1　 证明：等腰三角形两底角的平分线相等。

(引导学生分清条件和结论、画图、写出已知、求证。)

已知：如图，在△ABC中，AB＝AC，BD，CE是

△　　 ABC的角平分线。

求证：BD＝CE(一生口述证明过程，然后写出证明过程。)

证明：(略)

此题还有其它的证法吗？

(2)　　 你能证明等腰三角形两条腰上的中线相等吗？高呢？

　(引导学生分清条件和结论、画图、写出已知、求证并证明。其它证法合作交流完成。)