
1. 若锐角 有
有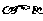 ,则下列各式中正确的是( )
,则下列各式中正确的是( )
A.  B.
B.
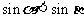
C.  D.
D.

4. 通过学习理解并学会“转化的思想”,“方程的思想”,提高分析能力、计算能力。
[例题分析]
例1. 如图,在RtΔABC中,∠C=90°。
(1)如果已知∠A和c,写出解ΔABC求未知元素的过程;
(2)如果已知a,b,写出解ΔABC求未知元素的过程;
(3)如果已知b,∠A,写出解ΔABC求未知元素的过程;
(4)如果已知a,∠B,写出解ΔABC求未知元素的过程。
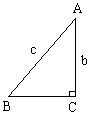
解:



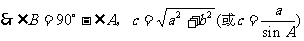
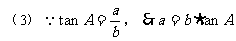





说明:
(1)从题中可见直角三角形中除直角以外的五个元素中,只要知道两个(其中至少有一个是边),我们就可以解这个三角形。
(2)在求某个元素时,可用方法不止一种时,最好用已知条件可直接求出的那种,这时算出的准确性高。像(2)、(3)、(4)小题中括号中结果都用到了解题过程中求出的数据,万一有错则直接影响到最后结果的正确性。
例2. 如图,在RtΔABC中,∠C=90°,AC=16,AC边上中线BD=17,解三角形ABC。(保留2个有效数字)

解:∵AC=16,BD为AC边上中线

在RtΔDBC中,由勾股定理得:

在RtΔABC中,由勾股定理得:
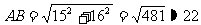


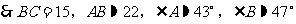
例3. 如图,已知ΔABC中,AB=4,AC=6,∠ABC=45°,求BC长及tanC。

分析:ΔABC不是直角三角形,我们应借助直角三角形来完成,要求tanC,又知∠ABC=45°,故应作BC边上的高AD,在RtΔADB和RtΔADC中,可分别求出BD、CD,问题就解决了。
解:过点A作AD⊥BC于D







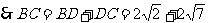

探讨:解决斜三角形边角的问题,一定要借助直角三角形才能解决。因此作三角形一边上的高是常作的辅助线,要熟练。
这道题我们充分利用了45°角的特殊性,除此以外,还可以过C点作CE⊥BA,交BA延长线于E,如图。

则RtΔBEC为等腰直角三角形,若设BE=EC=x



tanC则可在求出DC后求出。
例4. 如图,ΔABC中,∠BAC=45°,AD⊥BC于D,AD=8,BD=4,求DC和tan∠ACD。
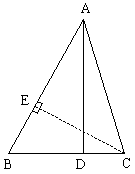
分析:条件中给了∠BAC=45°,而这个角不在直角三角形内,因此要设法将它放在直角三角形中,又已知条件中AD=8,BD=4,AB可求出。因此过C点作AB的垂线。
解:过C点作CE⊥AB于E
在RtΔADB中,由勾股定理,AD=8,BD=4
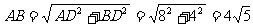
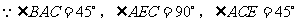






在RtΔADC中,由勾股定理:
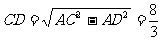

例5. 已知ΔABC中,AC=4,∠C=30°,AD为高,BD=1。求BC,AB,∠A,∠B。
分析:题目没有给出图形,我们要按照已知条件画图再求解。从条件看,已知一个锐角,这个角的一条边及另一边上的高,还有垂足到第三个顶点B的距离,而没有给出BC的长度,这样我们应该考虑到,D点可能在BC边上,也可能在BC的延长线上,此题应分两种情况求解。
解:如图,此题有两种情况。

在RtΔADC中,AC=4,∠C=30°


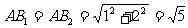


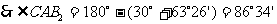
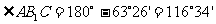
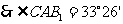
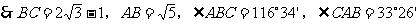
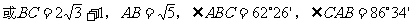
[模拟试题](答题时间:80分钟)
模拟练习一:
3. 任意三角形的高能把斜三角形中的边角关系转化到n个直角三角形之中,因此,要求我们会解有特殊角的斜三角形中的有关计算题。
2. 理解什么叫解直角三角形,并熟练掌握直角三角形的解法,并能按照题中条件画出符合条件的图形,写出正确的解题过程。
1. 熟练掌握直角三角形中三边的关系、两个锐角间的关系及边与锐角间的关系。并能根据直角三角形中给出的一些元素正确地选用这些关系,准确、迅速地求出其他元素。
4. 本节所学为锐角的四个三角函数,故它们的值都为正数,解题时不要忘记限定的条件是锐角。
[解直角三角形知识要点]
3. 弄清三角函数的增减性问题,是查表、比较大小、确定角或函数值的取值范围的关键。
2. 0°,30°,45°,60°,90°角的四个三角函数都要掌握好,在计算或化简中,要分清运算,分清大小,选择算法,准确求值。
1. 锐角的四个三角函数体现了三角形中边的比值与角的大小的一种对应关系,直角三角形中的边、角关系中,三者之中(角、两边)知二便可求。
5. 会利用学过的四个三角函数定义进行有关的计算和证明,会用有关锐角三角函数的知识解决一些求直角三角形中某个未知元素的简单问题。
[例题分析]
例1. 对比锐角的正弦与余弦的学习,谈一下你对正切、余切学习的认识。
解:(1)同正弦与余弦的定义一样,正切与余切也是在直角三角形中定义的。∠C=90°时,


它们与角度也有一一对应的关系。
(2)它们也具有类似于正弦、余弦值的变化规律,随着锐角α的增大,tanα的值也增大,而cotα的值反而减小,不同的是tanα是从0增大到不存在,它可以取到无穷大;而cotα则从不存在减少到0;因此在查表时要特别注意cotα的修正值的运用。
(3)从定义不难看出tanα与cotα互为倒数:
<1>tanαcotα=1
<2>而当α+β=90°时也有:tanα=cotβ,cosα=sinβ;


思考与探索:学了这四个三角函数后,我们知道当一个锐角确定后,它所在的直角三角形中任两条边的比值就确定了。我们规定了 那么对于sinA、cosA我们是否也可以对它们的倒数
那么对于sinA、cosA我们是否也可以对它们的倒数 进行规定呢?事实上,它们也是两个三角函数,我们将在今后的学习中见到它们。
进行规定呢?事实上,它们也是两个三角函数,我们将在今后的学习中见到它们。
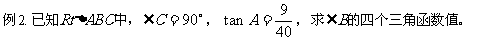
分析:所给条件是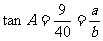 ,也就是知道了两条直角边的比值,凡已知比值的题,我们都可设一份为k,从而表达出各边的长度,从而完成解答。
,也就是知道了两条直角边的比值,凡已知比值的题,我们都可设一份为k,从而表达出各边的长度,从而完成解答。
解法一:设一份为k,
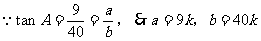



解法二:


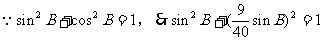
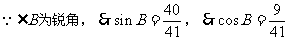
解法二不如解法一简单、直接,但它运用了互余两角的正、余切关系及同一角的三角函数间的关系,有助于我们对它们的理解和巩固。用多种方法解题,能开扩我们的思路。

分析:要求sinB的值,我们只要知道b与c间的关系,或∠B的度数。从已知可知,我们可根据定义转化已知条件为三角形的三边关系,再加上勾股定理,就可得出三边间关系,或者运用互余两角间关系,及同角三角函数间关系也可以求出sinB。
解法一:






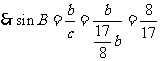
解法二:


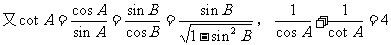



[正切和余切知识小结]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com