
3、探索思考:
观察课本第7页图1-5中⑴、⑵,你发现它们有什么共同特征,与同学交流。
把一个图形沿着某一条直线折叠,如果直线两旁的部分能够互相重合,那么称这个图形是轴对称图形,这条直线就是对称轴。
动手画出课本第5页两幅图的对称轴。
动手画出课本第7页图1-5中⑴、⑵的对称轴。
说说你所熟悉的哪些图形是轴对称图形,对称轴是什么?与同学讨论、交流,互相补充。
轴对称图形:圆、正方形、长方形、菱形、等腰梯形、等腰三角形、角、线段等。
学生口述对称轴的位置。
2、动手试一试:
画出课本第6页图1-1中⑴、⑵的对称轴。
体会课本第6页图1-3中对称轴与典型对称点。
课本第7页图1-4,切藕,如何摆放能使截面成轴对称?你能找出一些对称点吗?
1、观察、思考:
观察课本第6页图1-1中⑴、⑵,你能发现它们有什么共同特征,说出来与同学交流。
(折叠,重合)
仿课本图1-2进行操作,你有什么发现?(注意方法和要点的指导)
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么称这两个图形关于这条直线对称,也称这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做对称点。
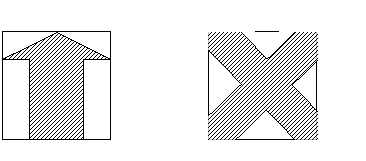 动手操作:用一张正方形的纸片,折叠后,把下列图形剪出来,并与同学交流你的剪法。
动手操作:用一张正方形的纸片,折叠后,把下列图形剪出来,并与同学交流你的剪法。
(几何画板动画:演示折叠方法)
通过本节课的教学,效果很好,特别是这节课的教案设计发挥了很大的作用,在教学过程中,我根据这个教案的设计,首先进行创设情境,通过活动,发现学生很容易被激发兴趣,从而增强对本节课的知识的探求欲,在具体探索过程中,学生积极参与活动,和组内同学进行了热烈地讨论交流且勇于思考,这样学生在交流中互相启发,相互激励,发展和完善自我。真正地达到了培养他们的合作精神的目的,由“学数学”向“做数学”过渡,提高了学生“做数学”的兴趣和能力;通过学生之间对话、师生对话,使知识在对话中生成,在交流中重组,在共享中拓展;通过讨论得出结果,体验讨论式学习的好处,享受成功的喜悦,也培养了学生综合分析问题的能力。
但是在这节课讲授过程中,也有不尽如人意的地方,主要体现在之前教案设计没有充分考虑到,如让学生尝试用自己的语言描述这些实物、图片的共同特征.有些学生就没有很好地贯彻老师的意图,只是简单地说了一下,没有认真地去思考,没有用自己的语言去认真的组织;还有学生的动手操作能力不够强,这一点在教案设计中没有好好的去研究。
总之这个教案设计是成功的,我将在以后的教案设计中认真地去总结,去完善,使得课堂教学能顺利的开展下去。
3.在欣赏现实生活中的轴对称图形之美时,体会轴对称在现实生活中的广泛运用和它的丰富的文化价值.
2.经历观察生活中的轴对称现象和轴对称图形,探索它们的共同特征的活动过程,发展空间观念。
1.通过这节课的学习,学生对轴对称和轴对称图形有了较为准确的理解,但学生的观察能力、语言表达能力还有待提高。
2.小剪刀一把,纸片2----3张,墨水1瓶。
●教学过程设计:
|
教师活动 |
学生活动 |
设计意图 |
|
1.创设情境 教师先展示纸折的飞机;剪纸作品(蝴蝶、五角星等);照片;实物;并用多媒体展示各种漂亮的轴对称图案等,然后让学生交流、展示各自收集的相关图片. 教师应关注以下几点: (1)学生参与活动是否积极主动,全神贯注; (2)学生自带的图片是否具有代表性; (3)审美意识和情感是否在感知中有所增强; (4)鼓励学生举出符合对称特征的物体:如风筝、知了、蜻蜓等。 |
学生欣赏图片,感知对称; 充分观察、讨论、交流, 尝试用自己的语言描述这些实物、图片的共同特征. |
让学生欣赏图片,充分感知对称,增加学生的审美意识,激发学生的学习欲望。 通过展示学生自带的图片,.让学生联系现实生活实际,主动参与数学活动,感知数学与生活密切相关。 使学生从这些图片中分别抽象出轴对称与轴对称图形的共同特征,并认识轴对称现象的广泛性。 |
|
教师活动 |
学生活动 |
设计意图 |
|
2.探索活动 活动一:折纸印墨迹 在纸的一侧滴一滴墨水后,对折,压平。 问题 1:你发现折痕两边的墨迹形状一样吗?为什么? 问题 2:两边墨迹的位置与折痕有什么关系? 问题3:联系实际,你能举出一些生活中图形成轴对称的实例吗? 问题4:你能正确地完成课本P8页的练习吗? |
学生动手、操作、观察、思考。组内同 学讨论、交流。 教师引导得出轴对称及对称轴、对称点的概念,并板书概念。 学生举例,处理练习。 |
通过学生观察、主动思考,认识轴对称的本质特征,鼓励学生善于观察、勇于发现,培养合作意识。 通过举例、练习,进一步认识轴对称的本质。 |
|
活动二:剪飞鸟图案 把一张长方形纸片对折,按课本图1-5剪出一个图案,然后再打开。 问题1:按照课本所示的方法剪纸,你得到了什么图案?它是轴对称图形吗?说出对称轴. 问题2:另取一张纸,对折两次,再仿照上面的过程画线、剪纸.你又得到什么图案?是轴对称图形吗?说出对称轴. 问题3:联系实际,你能举出一个轴对称图形的实例吗? 问题 4:你能正确地完成课本P9页第1题的练习吗? |
学生动手、操作、观察、思考。组内同学讨论、交流。并尝试着表述这些图形的共同特征。 教师归纳学生的表述,引导出轴对称图形及对称轴的概念,并板书概念。 学生举例,独立完成练习。 |
鼓励学生勇于发现,增强合作意识。培养学生的动手能力,观察能力和语言表达能力. 通过举例、练习,进一步认识轴对称图形的本质。 |
|
活动三: 问题 1: 根据课本图形1-2和1-4进行比较,轴对称与轴对称图形之间有什么区别吗? 问题 2: 如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形成轴对称吗?如果把两个成轴对称的图形看成一个整体,它是一个轴对称图形吗? |
学生根据两组图比较观察、思考、讨论、交流,教师引导学生得出其区别。 教师提出问题,学生思考,讨论交流,进一步明确轴对称与轴对称图形的区别和联系。 |
通过比较观察、相互讨论,进一步认识轴对称与轴对称图形的本质特征. 通过思考、讨论等活动,进行辨证唯物主义教育,让学生运用辨证的观点认识事物,进一步发展学生抽象思维的能力。 |
3.课堂练习: (1)图中的图形中是常见的安全标记,其中是轴对称图形的是( ) (1)图中的图形中是常见的安全标记,其中是轴对称图形的是( ) |
学生独立思考并完成解答。 |
培养学生的独立思考的能力和自主探索精神。 |
|
教师活动 |
学生活动 |
设计意图 |
(2)下面有4个汽车标致图案,其中是轴对称图形的是 ① ② ③ ④ ① ② ③ ④
A、②③④ B、①③④ C、①②④ D、①②③ (3)下列图形是轴对称图形码?若是,你能画出它们的对称轴吗? 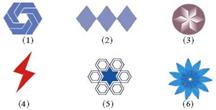  (4)数的运算中会有一些有趣的对称形式,如12×231=132×21,仿照这一形式,写出下列等式,并演算:12×462= , 18×891= 。 (5)小强站在镜前,从镜中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是 。  (6)如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图(一)中四边形ABCD就是一个“格点四边形”. (1)求图(一)中四边形ABCD的面积; (2)在图(二)方格纸中画一个格点三角形EFG,使△EFG的面积等于四边形ABCD的面积且为轴对称图形.   图(一) 图(二) |
学生独立思考并完成解答 |
培养学生的独立思考的能力和自主探索精神。 |
|
教师活动 |
学生活动 |
设计意图 |
|
4.课堂小结 这节课你学到了什么? |
学生自由发言,交流学习的经验和体会,并自主总结本节课的主要内容 |
培养学生的归纳能力和合作交流精神。使学生的知识系统化、条理化。 |
|
5.布置作业 《学习手册》 P1,1、2 |
|
巩固所学知识 |
●教学后记:
1、搜集轴对称图形图片、剪纸、折纸等.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com