
通过具体实例认识轴对称,探索它的基本性质,理解对应点所连的线段被对称轴垂直平分的性质。
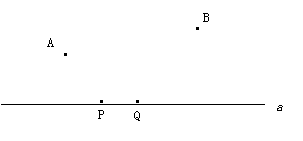
3、如图,A、B是直线L同侧的两定点,定长线段PQ在L上平行移动,问PQ移动到什么位置时,AP+PQ+QB的长最短?(画出图形,不要说明理由)
2、 如图,△ABC中,∠C=900。
如图,△ABC中,∠C=900。
⑴在BC上找一点D,使点D到AB的距离等于DC的长度;
⑵连结AD,画一个三角形与△ABC关于直线AD对称。
1、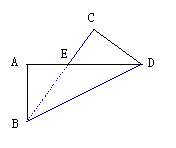 如图表示长方形纸片ABCD沿对角线BD进行折叠后的情况,图中有没有关于某条直线对称的图形?如有,请作出对称轴,图中是否有相等的线段、相等的角(不含直角)?如有,请写出相等的线段、相等的角.并说明理由。
如图表示长方形纸片ABCD沿对角线BD进行折叠后的情况,图中有没有关于某条直线对称的图形?如有,请作出对称轴,图中是否有相等的线段、相等的角(不含直角)?如有,请写出相等的线段、相等的角.并说明理由。
例1:判断题:
① 角是轴对称图形,对称轴是角的平分线; ( )
②等腰三角形至少有1条对称轴,至多有3条对称轴; ( )
③关于某直线对称的两个三角形一定是全等三角形; ( )
④两图形关于某直线对称,对称点一定在直线的两旁。 ( )
例2:下图曾被哈佛大学选为入学考试的试题.请在下列一组图形符号中找出它们所蕴含的内在规律,然后把图形空白处填上恰当的图形.
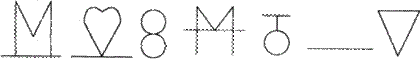
例3:如图,由小正方形组成的L形图中,请你用三种方法分别在下图中添画一个小正方形使它成为一个轴对称图形:
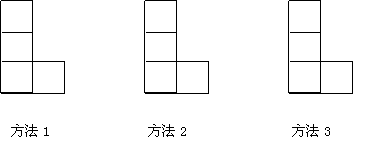
例4:如图,已知:ΔABC和直线l,请作出ΔABC关于直线l的对称三角形。
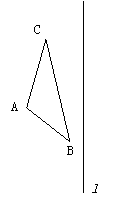
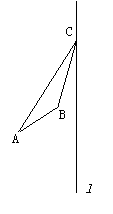
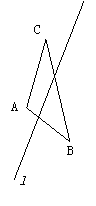
例5:如图,DA、CB是平面镜前同一发光点S发出的经平面镜反射后的反射光线,请通过画图确定发光点S的位置,并将光路图补充完整。
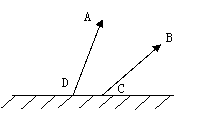
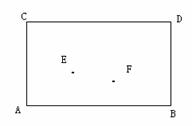
例6:如图,四边形ABCD是长方形弹子球台面,有黑白两球分别位于E、F两点位置上,试问怎样撞击黑球E,才能使黑球先碰撞台边AB反弹后再击中白球F?
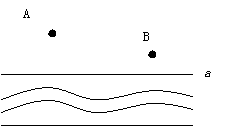
例7:如图,要在河边修建一个水泵站,向张庄A、李庄B送水。修在河边什么地方,可使使用的水管最短?
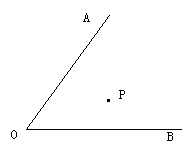
例8:如图,OA、OB是两条相交的公路,点P是一个邮电所,现想在OA、OB上各设立一个投递点,要想使邮电员每次投递路程最近,问投递点应设立在何处?
6.怎样画轴对称图形:
画轴对称图形时,应先确定对称轴,再找出对称点。
5.轴对称的性质:
⑴成轴对称的两个图形全等。
⑵如果两个图形成轴对称,那么对称轴是对称点连线的垂直平分线。
4. 线段的垂直平分线:
线段的垂直平分线:
垂直并且平分一条线段的直线,叫做这条线段的垂直平分线。
(也称线段的中垂线)
3.轴对称与轴对称图形的区别与联系:
区别:
①轴对称是指两个图形沿某直线对折能够完全重合,而轴对称图形是指一个图形的两个部分沿某直线对折能完全重合。
②轴对称是反映两个图形的特殊位置、大小关系;轴对称图形是反映一个图形的特性。
联系:
①两部分都完全重合,都有对称轴,都有对称点。
②如果把成轴对称的两个图形看成是一个整体,这个整体就是一个轴对称图形;如果把一个轴对称图形的两旁的部分看成两个图形,这两个部分图形就成轴对称。
常见的轴对称图形有:圆、正方形、长方形、菱形、等腰梯形、等腰三角形、等边三角形、角、线段、相交的两条直线等。
2. 什么叫轴对称图形:
如果把一个图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com