
数轴是非常要的数学工具,它的出现对数学的发展起了重要作用,它揭发了数和形的内在联系,很多数学问题都可以以它为基础,借助图直观地表示,为研究问题提供了新方法。
师生共同进行,什么是数轴,如何画数轴?如何在数轴上表示有理数?
六:小测(5分钟)
分层导学P8-2、3、4、5
七 本课作业 1, 预习P12~13,掌握怎样去求一个数的相反数,完成P13练习1
2,P18习题1.2第2、5题
3,选做分层导学P8--6、7;P93、4、5
1.2 数轴同步练习
第1题.  的相反数是______,
的相反数是______, 的相反数是______.
的相反数是______.
第2题. 如果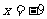 ,则
,则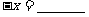 如果
如果 ,那么
,那么 .
.
第3题. 下列说法中错误的是( )
A.规定了原点、正方向和长度的直线叫数轴
B.数轴上的原点表示数零
C.在数轴上表示的数,右边的数总比左边的数大
D.所有的有理数都可以用数轴上的点表示
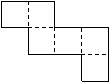
第4题. 如图,是一个正方体纸盒的展开图,请你任选三对非零的互为相反数,分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
第5题. 画一条数轴,并在数轴上表示下列各数,且用“<”号连接起来.
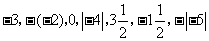
第6题. 点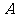 在数轴上距原点3个单位长度,且位于原点左侧,若将点
在数轴上距原点3个单位长度,且位于原点左侧,若将点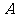 向右移动4个单位长度,再向左移动1个单位长度,此时点
向右移动4个单位长度,再向左移动1个单位长度,此时点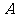 所表示的数是______;若点
所表示的数是______;若点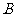 所表示的数是点
所表示的数是点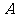 开始时所表示的数的相反数,作同样的移动以后,点
开始时所表示的数的相反数,作同样的移动以后,点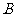 表示的数是______.
表示的数是______.
第7题. 用“<”把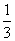 ,-
,-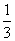 ,-
,-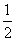 ,0,
,0, ,
,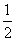 连接起来是____________________.
连接起来是____________________.
第8题. 下列各对数中,不是互为相反数的一对是
A.-(+5)和+(-5)
B.-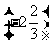 与
与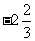
C.0和0
D.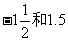
第9题. -(-100)的相反数是__________.
第10题. 有理数 ,
,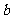 在数轴上的对应点的位置如下图所示.
在数轴上的对应点的位置如下图所示.
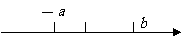
用不等号把 ,
,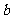 ,
, ,
, 连接起来.
连接起来.
第11题. 若 ,
,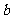 互为相反数,则下面四个等式中一定成立的是( )
互为相反数,则下面四个等式中一定成立的是( )
A. +
+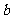 =0 B.
=0 B. +
+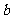 =1
=1
C.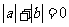 D.
D.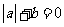
第12题. 下列结论正确的是( )
A.数轴上表示6的点与表示4的点相距10
B.数轴上表示+6的点与表示-4的点相距10
C.数轴上表示-4的点与表示4的点相距10
D.数轴上表示-6的点与表示-4的点相距10
第13题. 下列说法中,正确的是( )
A.正数和负数统称有理数
B.零是最小的有理数
C.倒数等于它本身的有理数只有1
D.互为相反数的两数之和为零
第14题. 在数轴上表示下列各数 并且“<”把它们连接起来.
并且“<”把它们连接起来.
第15题. - 的相反数是_____
的相反数是_____
第16题. 2的相反数是( )
A.2 B. C.
C.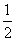 D.
D.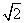
第17题.  的绝对值是( ).
的绝对值是( ).
A.2 B. C.
C. D.
D.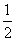
第18题. 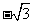 的相反数是 .
的相反数是 .
第19题. -3的相反数是
A.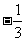 B.
B.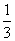 C.
C. D.
D.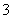
第20题. 1、如图,数轴上点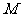 所表示的数的相反数为( )
所表示的数的相反数为( )
A.2.5 B.5 C.-2.5 D.-5
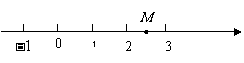
3、注意从学生的知识经验出发,充分发挥学生的主体意识,让学生主动参与学习活,并引导学生在课堂上感悟知识的生成,发展与变化,培养学生自主探索的学习方法。
2、教学过程突出了情竟到抽象到概括的主线,教学方法体了特殊到一般,数形结合的数学思想方法。
1、数轴是数形转化、结合的重要媒介,情境设计的原型来源于生活实际,学生易于体验和接受,让学生通过观察、思考和自己动手操作、经历和体验数轴的形成过程,加深对数轴概念的理解,同时培养学生的抽象和概括能力,也体出了从感性认识,到理性认识,到抽象概括的认识规律。
2.写出数轴上点A,B,C,D,E所表示的数:
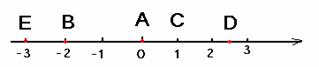
请大家回答下列问题: (出示投影4) (1)有人说一条直线是一条数轴,对不对?为什么? (2)下列所画数轴对不对?如果不对,指出错在哪里?
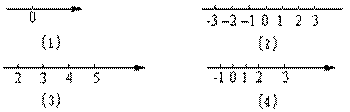
[教法说明]此组练习的目的是巩固数轴的概念. 十一、小结 本节课要求同学们能掌握数轴的三要素,正确地画出数轴,在此还要提醒同学们,所有的有理数都可用数轴上的点来表示,但是反过来不成立,即数轴上的点并不是都表示有理数,至于数轴上的哪些点不能表示有理数,这个问题以后再研究.
讲授新课
(出示投影1)
问题1:三个温度计.其中一个温度计的液面在0上2个刻度,一个温度计的液面在0下5个刻度,一个温度计的液面在0刻度. 师:三个温度计所表示的温度是多少? 生:2℃,-5℃,0℃. 问题2:在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.(小组讨论,交流合作,动手操作)
师:我们能否用类似的图形表示有理数呢? 师:这种表示数的图形就是今天我们要学的内容-数轴(板书课题). 师:与温度计类似,我们也可以在一条直线上画出刻度,标上读
数,用直线上的点表示正数、负数和零.具体方法如下
(边说边画): 1.画一条水平的直线,在这条直线上任取一点作为原点(通常取适中的位置,如果所需的都是正数,也可偏向左边)用这点表示0(相当于温度计上的0℃); 2.规定直线上从原点向右为正方向(箭头所指的方向),那么从原点向左为负方向(相当于温度计上0℃以上为正,0℃以下为负); 3.选取适当的长度作为单位长度,在直线上,从原点向右,每隔一个长度单位取一点,依次表示为1,2,3,…从原点向左,每隔一个长度单位取一点,依次表示为-1,-2,-3,… 师问:我们能不能用这条直线表示任何有理数?(可列举几个数)
让学生观察画好的直线,思考以下问题: (出示投影2) (1)原点表示什么数? (2)原点右方表示什么数?原点左方表示什么数? (3)表示+2的点在什么位置?表示-1的点在什么位置? (4)原点向右0.5个单位长度的A点表示什么数?
原点向左1.5个单位长度的B点表示什么数? 根据老师画图的步骤,学生思考在一条水平的直线上都画出什么?然后归纳出数轴的定义. 师:在此基础上,给出数轴的定义,即规定了原点、正方向和单
位长度的直线叫做数轴. 进而提问学生:在数轴上,已知一点P表示数-5,如果数轴上的原点不选在原来位置,而改选在另一位置,那么P对应的数是否还是-5?如果单位长度改变呢?如果直线的正方向改变呢? 通过上述提问,向学生指出:数轴的三要素--原点、正方向和单位长度,缺一不可.
[教法说明]通过“观察-类比-思考-概括-表达”展现知识的形成是从感性认识上升到理性认识的过程,让学生在获取知识的过程中,领会数学思想和思维方法,并有意识地训练学生归纳概括和口头表达能力. 师生同步画数轴,学生概括数轴三要素,师出示投影,生动手动脑练习
尝试反馈,巩固练习 (出示投影3).画出数轴并表示下列有理数:
1、1.5,-2.2,-2.5,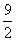 ,
,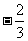 ,0.
,0.
从学生已有知识、经验出发研究新问题,是我们组织教学的一个重要原则。小学里曾学过利用射线上的点来表示数,为此我们可引导学生思考:把射线怎样做些改进就可以用来表示有理数?伴以温度计为模型,引出数轴的概念。教学中,数轴的三要素中的每一要素都要认真分析它的作用,使学生从直观认识上升到理性认识。直线、数轴都是非常抽象的数学概念,当然对初学者不宜讲的过多,但适当引导学生进行抽象的思维活动还是可行的。例如,向学生提问:在数轴上对应一亿万分之一的点,你能画出来吗?它是不是存在等。 四、教学目标 (一)知识与技能 1、掌握数轴的三要素,能正确画出数轴。 2、能将已知数在数轴上表示出来,能说出数轴上已知点所表示的数。 (二)过程与方法 1、使学生受到把实际问题抽象成数学问题的训练,逐步形成应用数学的意
识。 2、对学生渗透数形结合的思想方法。 (三)情感、态度与价值观 1、使学生初步了解数学来源于实践,反过来又服务于实践 的辩证唯物主
义观点。 2、通过画数轴,给学生以图形美的教育,同时由于数形的结合,学生会得
到和谐美的享受。 五、教学重点及难点 1、重点:正确掌握数轴画法和用数轴上的点表示有理数。 2、难点:有理数和数轴上的点的对应关系。 六、教学建议 1、重点、难点分析 本节的重点是初步理解数形结合的思想方法,正确掌握数轴画法和用数轴上的点表示有理数,并会比较有理数的大小.难点是正确理解有理数与数轴上点的对应关系。数轴的概念包含两个内容,一是数轴的三要素:原点、正方向、单位长度缺一不可,二是这三个要素都是规定的。另外应该明确的是,所有的有理数都可用数轴上的点表示,但数轴上的点所表示的数并不都是有理数。通过学习,使学生初步掌握用数轴解决问题的方法,为今后充分利用“数轴”这个工具打下基础。 2、知识结构 有了数轴,数和形得到了初步结合,这有利于对数学问题的研究,数形结合是理解数学、学好数学的重要思想方法,本课知识要点如下: 定 义 规定了原点、正方向、单位长度的直线叫数轴 三要素 原 点 正方向 单位长度 应 用 数形结合
人教版七年级(上册)第一章有理数1.2有理数1.2.2数轴。这一节是初中数学中非常重要的内容,从知识上讲,数轴是数学学习和研究的重要工具,它主要应用于绝对值概念的理解,有理数运算法则的推导,及不等式的求解。同时,也是学习直角坐标系的基础,从思想方法上讲,数轴是数形结合的起点,而数形结合是学生理解数学、学好数学的重要思想方法。日常生活中带见的用温度计度量温度,已为学习数轴概念打下了一定的基础。通过问题情境类比得到数轴的概念,是这节课的主要学习方法。同时,数轴又能将数的分类直观的表现出来,是学生领悟分类思想的基础。 二、学生学习情况分析 (1)知识掌握上,七年级的学生刚刚学习有理数中的正负数,对正负数的概念理解不一定很深刻,许多学生容易造成知识遗忘,所以应全面系统的去讲述; (2)学生学习本节课的知识障碍。学生对数轴概念和数轴的三要素,学生不易理解,容易造成画图中掉三落四的现象,所以教学中教师应予以简单明白、深入浅出的分析; (3)由于七年级学生的理解能力和思维特征和生理特征,学生的好动性,注意力容易分散,爱发表见解,希望得到老师的表扬等特点,所以在教学中应抓住学生这一生理心理特点,一方面要运用直观生动的形象,一发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面要创造条件和机会,让学生发表见解,发挥学生的主动性。
(六) 布置作业,巩固与提高并举
P43 2 3
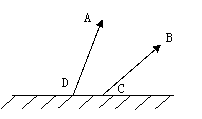 思考题:如图,DA、CB是平面镜前同一发光点S发出的经平面镜反射后的反射光线,请通过画图确定发光点S的位置,并将光路图补充完整.
思考题:如图,DA、CB是平面镜前同一发光点S发出的经平面镜反射后的反射光线,请通过画图确定发光点S的位置,并将光路图补充完整.
[设计说明:巩固新知识,运用新知识,让课堂延伸到学生生活的每一个角落,在学中做,在做中学,不断的提高自己的水平;本题要在深刻理解轴对称图形的概念的基础上才能完成,可供学有余力的同学课后思考]
 注:备选题
注:备选题
1、右图是从镜中看到的一串数字,这串数字应为 .
2、数的运算中有一些有趣的对称式,如12×231=132×21,请你仿照这个等式填空:__________×462=__________×__________.
3、如图,△ABC中,∠C=900
 ⑴在BC上找一点D,使点D到AB的距离等于DC的长度;
⑴在BC上找一点D,使点D到AB的距离等于DC的长度;
⑵连结AD,画一个三角形与△ABC关于直线AD对称.
4、已知:如图,CDEF是一个矩形的台球面,有黑白两球分别位于点A、B两点,试问怎样撞击黑球A,使A先碰到台边EF反弹后再击中白球B?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com