1.图1表示甲、乙两山坡情况,其中tanα_____tanβ,_____坡更陡.(前一空填“>”“<”或“=”,后一空填“甲”“乙”)

图1

2. 30°，45°，60°角的三角函数值

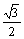[基础练习]一、1. ，； 2. 1 - ； 3. ∠A = 60°，∠B = 45°. 二、1. B； 2. B. 三、1.(1)；(2). . 2.(1)30°；(2)50°.

[综合练习]AB = 15cm.

[探究练习]sin15°= 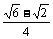，cos15°= ，tan15°= 2 -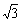；sin75°= ，cos75°= 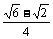，tan75°= 2 +.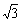

2.求满足下列各式的锐角α：

(1)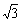tanα-1 = 0；　　　　 　　　(2)2cos (α-20°) = .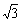

[综合练习]

已知：如图1-4，△ABC中，∠C = 90°，D是AC边上一点，∠BDC = 45°，CD = 6cm，sinA = . 求斜边AB的长.

[探究练习]

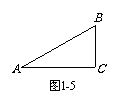如图1-5，△ABC中，∠C = 90°，∠A = 30°，你能利用这个图形分别求出15°和75°角的三个三角函数值吗？

1.求下列各式的值：

(1)2sin30°+ cos60°+ tan45°；　　 (2)；

2.如果cosA = ，那么锐角A的取值范围是(　　 )；

A. 0°< A < 30°　　　　　　　　　　 B. 30°< A < 45°

C. 45°< A < 60°　　　　　　　　　　 D. 60°< A < 90°

1.下列不等式成立的是(　　 )；

A. sin30°< cos45°< tan30°　　　　 B. cos60°< sin45°< tan45°

C. tan30°< sin30°< cos45°　　　　 D. tan60°< cos45°< sin60°

3.若|2sinA -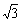|+ (tanB -1)² = 0，则∠A = 　　　°，∠B = 　　　°.

2. = 　　　　；

1.sin30°+ cos45°= 　　　　，cos45°sin²30°+ sin²60°= 　　　　；

2.　　　 对自己本节课的学习情况进行评价.(探索规律的一般方法；探索过程中哪些量是

重要的；探索规律的一般过程等)

(教师通过提问的方式小结本节知识，提高了学生学习的积极性，丰富了“主角”意识，使学生悟出得结论的过程，积累数学活动经验，养成提出问题--进行猜想--探索验证--总结结论--应用结论的良好学习习惯.)