2、议一议：

观察下列三组命题，它们的条件和结论之间有怎样的关系？

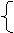如果两个角是对顶角，那么它们相等。

如果两个角相等，那么它们是对顶角。

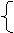如果小明患了肺炎，那么他一定会发烧。

如果小明发烧，那么他一定患了肺炎。

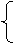三角形中相等的边所对的角相等。

三角形中相等的角所对的边相等。

(引导学生观察这些成对命题的条件和结论之间的关系，归纳出它们的共性，进一步得出“互逆定理”的概念。)

1、问题情境：在一个三角形中，当两边的平方和等于第三边的平方时，我们曾用度量的方法得出“这个三角形是直角三角形”的结论，你能证明这个结论吗？

已知：在ΔABC中，AB²+AC²=BC²

求证：ΔABC是直角三角形

a)　　　 (！)　　　　　 (2)

　　　 (讲解证明思路及证明过程，引导学生领会证明思路及证明过程，得出结论。)

结论：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

1、你记得勾股定理的内容吗？你曾经用什么方法得到了勾股定理？

(由学生回顾得出勾股定理的内容。)

定理：直角三角形两条直角边的平方和等于斜边的平方。

4、 一条直角边和另一条直角边上的中线队以相等的两个直角三角形全等。

随堂练习：

随堂练习1．

议一议

　 如图：已知∠ACB=∠BDA=90^。

要使 ⊿ACB≌⊿BDA，还需要什么

条件？把他们写出来，并说明

理由。

课堂小结：

本节课通过问题的牵引，小组合作讨论．探究出证明直角三角形的方法“HL”．再在实际问题中运用．加深理解，拓展思维，提高综合分析能力和书写表达能力。综合开放性试题培养大家的探究意识．

作业：

课本习题1．5　 1、2

3、 两条直角边对应相等的两个直角三角形全等。

2、 斜边及一锐角对应相等的两个直角三角形全等。

1、 锐角对应相等的两个直角三角形全等。

2、判定直角三角形的方法有哪些，分别说出？(HL,SAS,ASA,AAS,SSS.先考虑HL,在考虑另外四种方法。)

做一做 如图利用刻度尺和三角板，能否

做出这个角的角平分线？并证明。

练习 　随堂练习P23--1

　 判断命题的真假，并说明理由

3．关键：引导学生着重分析证明的思路和方法，注意书写表达的规范性。

教学过程：

两边及其一个角对应相等的两个三角形全等吗？如果相等说明理由。如果不相等，应如何改变条件？用自己的语言清楚地说明，并写出证明过程。

问题1，此定理适用于什么样的三角形？(适用于直角三角形)

2．难点；用数学的语言清楚地表达自己的想法，正确的表达书写证明过程。