3、结合具体例子了解逆命题的概念，会识别两个互逆命题，知道原命题成立其逆命题不一定成立。

教学过程：

引入：我们曾经利用数方格和割补图形的方未能得到了勾股定理。实际上，利用公理及其推导出的定理，我们能够证明勾股定理。

定理：直角三角形两条直角边的平方和等于斜边的平方。

如图，在△ABC中，∠C=90°，BC=a，AC=b，AB=c，

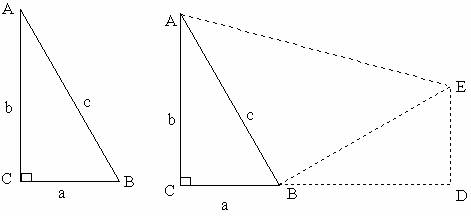
延长CB至点D，使BD=b，作∠EBD=∠A，并取BE=c，连接ED、AE，则△ABC≌△BED。

∴∠BDE=90°，ED=a(全等三角形的对应角相等，对应边相等)。

∴四边形ACDE是直角梯形。

∴S_梯形ACDE =(a+b)(a-b)= (a+b)²

∴∠ABE=180°-∠ABC-∠EBD=180°- 90°=90°

AB=BE

∴S_△ABC = c²

∵S_梯形ACDE = S_△ABE +S_△ABC+ S_△BED ,

∴(a+b)²=c²+ab+ab　　　　 即a²+ab+b²=c²+ab+ab

∴a²+b²=c²

反过来，在一个三角形中，当两边的平方和等于第三边的平方时，我们曾用度量的方法得出“这个三角形是直角三角形”的结论，你能证明这个结论吗？

已知：如图，在△ABC，AB²+AC²=BC²，求证：△ABC是直角三角形。

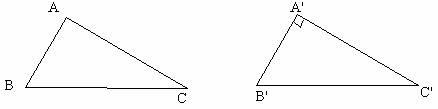
证明：作出Rt△A’B’C’，使∠A=90°，A’B’=AB，A’C’=AC，则

A’B’²+A’C’²=B’C’²　 (勾股定理)

∵AB²+AC²=BC²　 ，A’B’=AB，A’C’=AC，

∴BC²= B’C’²

∴BC=B’C’

∴△ABC≌△A’B’C’　 (SSS)

∴∠A=∠A’=90°(全等三角形的对应角相等)

因此，△ABC是直角三角形。

定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

在两个命题中，如果一个命题的条件和结论分别是另一个命题的结论和条件，那么这两个命题称为另一个命题的互逆命题，其中一个命题称为另一个命题的逆命题。

一个命题是真命题，它的逆命题却不一定是真命题。如果一个定理的逆命题经过证明是真命题，那么它也是一个定理。这两个定理称为互逆定理，其中一个定理称为另一个定理的逆定理。

练习题：随堂作业

作业：P20：1、2、3

2、了解勾股定理及其逆定理的证明方未能，能够证明直角三角形全等的“HL”判定定理。

1、进一步掌握推理证明的方法，发展演绎推理能力。

3、预习作业：P21-22页　 做一做

板书设计：

课后记：

2、拓展作业：《目标检测》

1、基础作业：P20页习题1.4　 1、2、3。

6、课堂小结：本节课你都掌握了哪些内容？

(引导学生归纳总结，互逆定理的定义及相互间的关系。)

4、练习：

(1)　　 写出命题“如果有两个有理数相等，那么它们的平方相等”的逆命题，并判断是否是真命题。

(2)　　 试着举出一些其它的例子。

(3)　　 随堂练习 1

3、关于互逆命题和互逆定理。

　 (1)在两个命题中，如果一个命题的条件和结论分别是另一个命题的结论和条件，那么这两个命题称为互逆命题，其中一个命题称为另一个命题的逆命题。

　 (2)一个命题是真命题，它的逆命题却不一定是真命题。如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，这两个定理称为互逆定理，其中一个定理称为另一个定理的逆定理。

(引导学生理解掌握互逆命题的定义。)