
4、练习:
写出命题“如果有两个有理数相等,那么它们的平方相等”的逆命题,并判断是否是真命题。
试着举出一些其它的例子。
随堂练习 1
3、关于互逆命题和互逆定理。
(1)在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题。
(2)一个命题是真命题,它的逆命题却不一定是真命题。如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理。
(引导学生理解掌握互逆命题的定义。)
问题情境:在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量的方法得出“这个三角形是直角三角形”的结论,你能证明这个结论吗?
已知:在ΔABC中,AB2+AC2=BC2
求证:ΔABC是直角三角形
(!) (2)


(讲解证明思路及证明过程,引导学生领会证明思路及证明过程,得出结论。)
结论:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
2、议一议:
观察下列三组命题,它们的条件和结论之间有怎样的关系?
 如果两个角是对顶角,那么它们相等。
如果两个角是对顶角,那么它们相等。
如果两个角相等,那么它们是对顶角。
 如果小明患了肺炎,那么他一定会发烧。
如果小明患了肺炎,那么他一定会发烧。
如果小明发烧,那么他一定患了肺炎。
 三角形中相等的边所对的角相等。
三角形中相等的边所对的角相等。
三角形中相等的角所对的边相等。
(引导学生观察这些成对命题的条件和结论之间的关系,归纳出它们的共性,进一步得出“互逆定理”的概念。)
1、你记得勾股定理的内容吗?你曾经用什么方法得到了勾股定理?
(由学生回顾得出勾股定理的内容。)
定理:直角三角形两条直角边的平方和等于斜边的平方。
2、全等三角形的证明。
新授:
引入:两边及其中一边的对角对应相等的两个三角形全等吗?如果其中一边所对的角是直角呢?
定理:斜边和一条直角边对应相等的两个直角三角形全等。
这一定理可以简单地用“斜边、直角边”或“HL”表示。
已知:如图,△ABC和△A’B’C’中∠C=∠C’=90°,且AB=A’B’,BC=B’C’,
求证:△ABC≌△A’B’C’
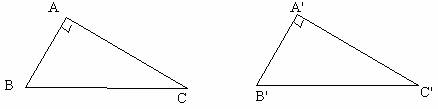
证明:Rt△ABC和Rt△A’B’C’中,
∵AB=A’B’,BC=B’C’,AC2=BC2-AB2 , A’C’2=B’C’2-A’B’2
∵AC2=A’C’2 ∴AC=A’C’
∴△ABC ≌A’B’C’(SSS)
做一做:
用三角尺可以作角平线,如图,在已知∠AOB的两边上分别取点M、N,使OM=ON,再过点M作OA的垂线,过点N作OB的垂线,两垂线交于点P,那么射线OP就是∠AOB的平分线
请证明:
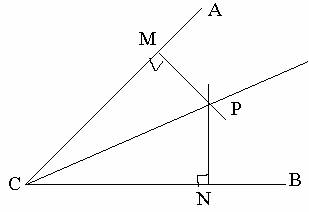
证明: ∵MC=NC PC=PC
∴Rt△MCP≌Rt△NCP (HL)
∴∠MCP=∠NCP(全等三角形对应角相等)
议一议:如图,已知∠ACB=BDA=90°,要使△ACB≌△BDA,还需要什么条件?把它们分别写出来。

随堂练习
判断下列命题的真假,并说明理由。
(1)两个锐角对应相等的两个直角三角形全等。
(2)斜边及一锐角对应相等的两个直角三角形全等。
(3)两条直角边对应相等的两个直角三角形全等。
(4)一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等。
作业:P23 1、2
1、勾股定理即其逆定理。
3、结合具体例子了解逆命题的概念,会识别两个互逆命题,知道原命题成立其逆命题不一定成立。
教学过程:
复习:
2、了解勾股定理及其逆定理的证明方未能,能够证明直角三角形全等的“HL”判定定理。
1、进一步掌握推理证明的方法,发展演绎推理能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com