
1.命题“两条平行线被第三条直线所截,同位角相等”的逆命题是 ;
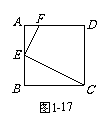 已知:如图1-17,在正方形ABCD中,E为AB的中点,F为AD上一点,且AF =
已知:如图1-17,在正方形ABCD中,E为AB的中点,F为AD上一点,且AF = 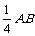 ,求证:CE⊥EF.
,求证:CE⊥EF.
|
纠正错解 |
|
|
|
点 评 |
|
|
[综合练习]
 如图1-18,沿AE折叠矩形ABCD,使点B落在CD边上的点F处,已知AB =
10cm, BC = 8cm, 连接EF, 求EF的长.
如图1-18,沿AE折叠矩形ABCD,使点B落在CD边上的点F处,已知AB =
10cm, BC = 8cm, 连接EF, 求EF的长.
[探究练习]
已知:直角三角形三边的长都是正整数,其中一条直角边的长为21cm,求此直角三角形周长的最小值.
2. 直角三角形
练习一
[基础练习] 一、1. 3; 2. 3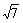 cm. 二、1. B; 2. C. 三、提示:连接CF, 证EF2 + CE2 = CF2.
cm. 二、1. B; 2. C. 三、提示:连接CF, 证EF2 + CE2 = CF2.
[综合练习]5cm.
[探究练习]70cm. 提示:设斜边为c, 一条直角边为a, 由c2 - a2 = 212 = 1×441 = 3×147 = 7×63 = 9×49知a + c = 49.
2.若三角形三个内角的度数之比为1︰2︰3,则此三角形三个内角的对边长度之比为( ).
A. 1︰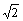 ︰
︰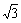 B. 1︰2︰3
B. 1︰2︰3
C. 1︰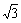 ︰2
D. 3︰4︰5
︰2
D. 3︰4︰5
1.已知三条线段的长度之比为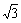 ︰
︰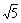 ︰2
︰2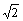 ,那么这三条线段( );
,那么这三条线段( );
A. 能构成锐角三角形 B. 能构成直角三角形
C. 能构成钝角三角形 D. 不能构成三角形
2.已知:△ABC中,∠A = 60°, AB = 9cm, AC = 6cm, 则BC = .
1.如图1-16,已知:△ABC中,∠C = 90°, AD是∠BAC的平
分线,CD = 1.5cm, BD = 2.5cm, 则AC = cm;
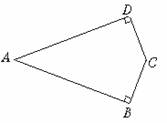
3.如下图,已知∠ABC=∠ADC=90°,E是AC上一点,AB=AD,求证:EB=ED.
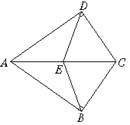
2.已知:如下图,CD、C′D′分别是Rt△ABC,Rt△A′B′C′斜边上的高,且CB=
C′B′,CD=C′D′.求证:△ABC≌△A′B′C′.
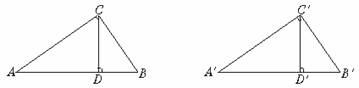
1.如下图,CD⊥AD,CB⊥AB,AB=AD,求证:CD=CB.
3.下列条件不可以判定两个直角三角形全等的是
A.两条直角边对应相等 B.有两条边对应相等
C.一条边和一锐角对应相等 D.一条边和一个角对应相等
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com