
3. 结合具体例子了解逆命题的概念,会识别两个互逆命题,知道原命题成立逆命题不一定成立.
2. 了解勾股定理及其逆定理的证明方法.
1. 进一步掌握推理证明的方法,发展演绎推理能力.
中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫作股,斜边叫做弦.据《周髀算经》记载,西周开国时期(约公元前1千多年)有个叫商高的人对周公说,把一根直尺折成直角,两端连接得一个直角三角形,如果勾是3,股是4,那么弦等于5.
人们还发现,在直角三角形中,勾是6,股是8,弦一定是10;勾是5,股是12,弦一定是13,等等.即32+42=52,62+82=102,52+122=132,…,勾2+股2=弦2. 是不是所有的直角三角形都具有这个性质呢?世界上许多数学家,先后用不同方法证明了这一性质.我国把它称为勾股定理.
直角三角形是一种特殊的三角形,它有许多重要性质.在前面几节中,我们曾介绍过直角三角形的一个性质:30°的角所对的直角边等于斜边的一半.这一节所研究的勾股定理,也是直角三角形的性质,而且是一条非常重要的性质,在以后的学习中,将利用勾股定理及直角三角形的其他一些性质,研究直角三角形中一些计算问题.因此,本节是这一章的重要内容,也是我们以后学习的基础.
2.已知:△ABC中,AB = 13, BC = 10, BC边上的中线AD = 12. 求证:△ABC是等腰三角形.
[综合练习]
 如图1-20,Rt△ABC中,AB = AC, D是斜边BC的中点,E、F分别是AB、AC上的点,且DE⊥DF. 若BE = 12cm, CF = 5cm, 求△DEF的面积.
如图1-20,Rt△ABC中,AB = AC, D是斜边BC的中点,E、F分别是AB、AC上的点,且DE⊥DF. 若BE = 12cm, CF = 5cm, 求△DEF的面积.
[探究练习]
我们知道,命题“直角三角形斜边上的高是它分斜边所成的两条线段的比例中项”是一个真命题,试写出它的逆命题,并判断它是否是真命题,如果是,请给出证明;如果不是,请说明理由.
|
纠正错解 |
|
|
|
点 评 |
|
|
练习二
[基础练习] 一、1. 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行; 2.假,正方形是矩形,真; 二、1. B; 2. D. 三、1. 75 cm2;2. 提示:证△ABD是直角三角形.
cm2;2. 提示:证△ABD是直角三角形.
[综合练习]12cm2.
[探究练习](略)
1.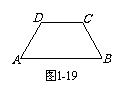 已知:如图,梯形ABCD中,AB∥DC, BC = CD = DA = = 10cm. 试求该梯形的面积.
已知:如图,梯形ABCD中,AB∥DC, BC = CD = DA = = 10cm. 试求该梯形的面积.
2.若直角三角形两直角边上的中线长分别为5cm和2 cm,则这个直角三角形的斜边长为( ).
cm,则这个直角三角形的斜边长为( ).
A. 10cm B. 4 cm C.
cm C.  cm D. 2
cm D. 2 cm
cm
1.若等腰三角形的顶角是120°,底边长为2cm,则它的腰长等于( );
A.  cm B.
cm B.  cm C. 2cm D.
cm C. 2cm D.  cm
cm
2.命题“矩形是正方形”是一个 命题,它的逆命题是 ,
这是一个 命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com