
1、用三角尺可以按下面的方法画角平分线:已知∠AOB,在OA、OB上分别取点E、F,使OE=OF再分别过点E、F画OA、OB的垂线,这两条垂线相交于点C,画射线O(如图),试证明射线OC平分∠AOB.


由上图,如果∠BAC=∠B’A’C’=30°,那么△ABB’是什么三角形?△ABC(或△A’B’C’)
的三条边之间有什么关系?
如图,如果∠BAC=30°,那么BC和AB之间有什么样的数量关系?(BC=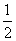 AB)你能证明这个结论吗?(就用上面的拼图)
AB)你能证明这个结论吗?(就用上面的拼图)

2、如何证明你的结论
引导学生根据命题画出图形
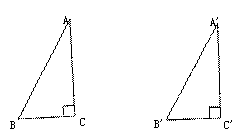
写出已知、求证
已知:如图,在△ABC和△A’B’C’中,∠ACB=∠A’C’B’=90°,AB=A’B’,AC=A’C’,
求证:△ABC≌△A’B’C’.
分析:上节课我们是用什么方法来证明等腰三角形的性质和判定的(把等腰三角形拆分成两个直角三角形,然后证它们全等),那么我们现在根据这两个直角三角形的具备的条件,可以考虑怎样证明它们全等 ?(把两个直角三角形拼合成一个等腰三角形,再运用等腰三角形的性质)

引导学生分析证题思路,并完成证明过成.
概括直角三角形全等的判定“HL”定理
1、用操作的方法证实你的猜想(按条件作一个直角三角形,然后相互比较是否一样,合情推理).
问题一:直角三角形全等的条件有哪些?
一般三角形全等的判定方法可以判定直角三角形全等,由于直角三角形是特殊的三角形,所以还有一般三角形所没有的特殊性的判定方法.
问题二:你认为具备这样条件的两个直角三角形一定全等吗?为什么?
即,斜边和一条直角边对应相等的两个直角三角形全等吗?
3. 已知:如图5,AD⊥BE,
垂足C是BE的中点,AB=DE.
求证:AB∥DE. 图5
2. 要测量河两岸相对角的两点A、B的距离,先在AB的垂线BF上取
两点C、D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线
上(如图4),可以证明△EDC≌△ABC,使ED=AB,因此测得ED的长就是
 AB的长,判定△EDC≌△ABC的理由是( ).
AB的长,判定△EDC≌△ABC的理由是( ).
A.边角边公理 B.角边角公理 C.边边边公理 D.斜边、直角边公理
1. 在Rt△ABC中,∠C=90°,CD是AB边上的中线,延长CD到E使DE=CD,连结AE,图中有________对全等三角形.
在Rt△ABC中,∠C=90°,CD是AB边上的中线,延长CD到E使DE=CD,连结AE,图中有________对全等三角形.
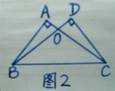
3. 已知:如图2,∠A=∠D=90°,CD是AB边上的中线,延长CD到E
使DE=CD,连结AE,图中有_____对全等三角形.
练 习二
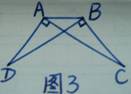 已知:如图3,AD=BC,AD⊥AC,BC⊥BD.
已知:如图3,AD=BC,AD⊥AC,BC⊥BD.
求证:AC=BD
2. AD、A′D′分别是锐角△ABC和△A′B′C′中BC、B′C′边上的高,且AB= A′B′,AD= A′D′,若使△ABC≌△A′B′C′,请你补充条件___(只需填写一个你认为适当的条件).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com