本节重点是对上一节所学内容--线段的垂直平分线的性质定理及判定定理的运用，有一定难度.所以在本节中，教科书尽可能创设一些问题情境，为学生提供自主探索发现的空间，然后再进行证明，从而将证明作为探索活动的自然延续和必要发展，使学生经历“探索--发现--猜想--证明”的过程，体会合情推理与演绎推理在获得结论中积极各自发挥的作用.

3. 如图6，在△ABC中，∠C=90°，BD平分∠ABC交AC于D，

DE是斜边AB的垂直平分线，且DE=1cm,求AC的长度.　　

　　　　　　　　　　　　　　　　 图6

2.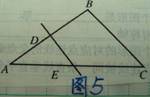 已知：如图5，在△ABC中，AB的中垂线交AC于点E，

若AE=2，则B、E两点间的距离__________　　　　　 　　　　

1. 已知：如图4，AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论：

(1) ∠C=72 °； (2)BD是∠ABC的平分线；(3) △ABD是等腰三角形.

其中正确的有(　　 )　　 　　　　　　　　　　　　　　

A. 3个　 B.2个　 C. 1个　 D. 0个　　　　　　　　　　　　　　　　　　　　　　 图4

3. 如图2，ABCD是正方形，△PAD是等边三角形，则∠BPC为_______.

A. 15°　 B. 20°　 C. 25°　 D. 30°

　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　图2

练习二

如图3，在△ABC中，∠BAC=80°，AB,AC的垂直平分线分别

交BC于D、E

求∠EAD的度数.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图3

2.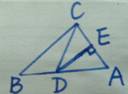 已知：如图1，DE是AC的垂直平分线，AB=12cm，BC=10cm,则三角形BCD的周长为_________.

A. 22cm　 B. 16cm　 C.26cm　 D.25cm

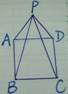　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　图1

练 习一

1. 在△ABC中，AB=AC，∠A=40°,AB的垂直平分线MN交AC于D，则∠DBC=__________.

正确理解线段垂直平分线性质定理及判定定理的条件和结论，运用时要注重联系等腰三角形及直角三角形的性质，提高综合运用知识的能力.应用线段垂直平分线的性质定理可证明线段的等量关系，从而可不完全依赖全等三角形证明线段或角相等.

2. 能够利用尺规作出已知线段的垂直平分线.

1. 掌握线段的垂直平分线的性质定理及判定定理，并能够证明.