
1.3三角函数的有关计算(二)
教学目标
知识与能力目标
能够用计算器进行有关三角函数值的计算.能够运用计算器辅助解决含三角函数值计算的实际问题.
过程与方法目标
经历用计算器由已知锐角求三角函数值的过程.进一步体会三角函数的意义;借助计算器,解决含三角函数的实际问题,提高用现代工具解决实际问题的能力,发现实际问题中的边角关系,提高学生有条理地思考和表达的能力.
情感与价值观要求
通过积极参与数学活动,体会解决问题后的快乐. 感悟计算器的计算功能和三角函数的应用价值
教学重点、难点
用计算器由已知锐角求三角函数值及用计算器辅助解决含三角函数值计算的实际问题.
 教学过程
教学过程
创设问题情境,引入新课
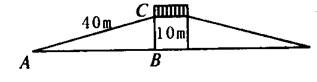
随着人民生活水平的提高,农用小轿车越来越多,为了交通安全,某市政府要修建10 m高的天桥,为了方便行人推车过天桥,需在天桥两端修建40m长的斜道.这条斜道的倾斜角是多少?
解:在Rt△ABC中,BC=10 m,AC=40 m,
sinA=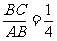 .可是我求不出∠A.
.可是我求不出∠A.
问题:我们知道,给定一个锐角的度数,这个锐角的三角函数值都唯一确定.给定一个锐角的三角函数值,这个锐角的大小也唯一确定吗?为什么?
根据HL定理可知这样的直角三角形形状和大小是唯一确定的,当然∠A的大小也是唯一确定的.
我们知道了sinA= 时,锐角A是唯一确定的.现在我要告诉大家的是要解决这个问题,我们可以借助于科学计算器来完成.这节课,我们就来学习如何用科学计算器由锐角三角函数值求相应锐角的大小.
时,锐角A是唯一确定的.现在我要告诉大家的是要解决这个问题,我们可以借助于科学计算器来完成.这节课,我们就来学习如何用科学计算器由锐角三角函数值求相应锐角的大小.
师生互动、学习新课
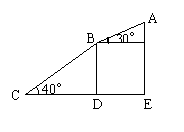
2.求图中避雷针CD的长度.(精确到0.01米)

1. 一个人从山底爬到山顶,需先爬40°的山坡300米,再爬30°的山坡100米,求山高.(结果精确到0.01米)
一个人从山底爬到山顶,需先爬40°的山坡300米,再爬30°的山坡100米,求山高.(结果精确到0.01米)
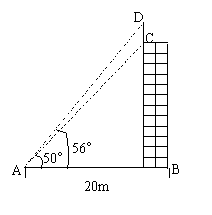
2.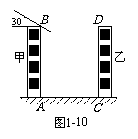 图1-10,住宅区内两栋楼的高AB = CD = 30m,两楼间的距离AC = 24m,现需了解甲楼对乙楼采光的影响情况,当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高(精确到0.1m).
图1-10,住宅区内两栋楼的高AB = CD = 30m,两楼间的距离AC = 24m,现需了解甲楼对乙楼采光的影响情况,当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高(精确到0.1m).
[综合练习]
 如图1-11,起重机的机身AD高21m,吊杆AB长36m,吊杆与水平线的夹角∠BAC可在30°-80°的范围内变化,求这台起重机工作时吊杆端点C离地面的最大高度和离机身的最大水平距离(精确到0.1m).
如图1-11,起重机的机身AD高21m,吊杆AB长36m,吊杆与水平线的夹角∠BAC可在30°-80°的范围内变化,求这台起重机工作时吊杆端点C离地面的最大高度和离机身的最大水平距离(精确到0.1m).
练习二
[基础练习]一、1. 6.3米,9.8米;2. 1097米. 二、1. D;2. A. 三、1. 12.5米. 2. 16.1m.
[综合练习]最大高度约56.5米,最大水平距离约31.2米.
1.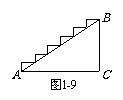 如图1-9,某宾馆在楼梯上铺地毯,楼梯面AB与地面AC的夹角为34°,若楼梯面AB长9米,问:地毯至少需多少米长(精确到0.1米)?
如图1-9,某宾馆在楼梯上铺地毯,楼梯面AB与地面AC的夹角为34°,若楼梯面AB长9米,问:地毯至少需多少米长(精确到0.1米)?
2.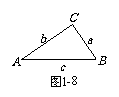 如图1-8,△ABC中,∠C = 90°,则以下各式正确的是( );
如图1-8,△ABC中,∠C = 90°,则以下各式正确的是( );
A. a = c·sinA,b = c·cosA B. a = ,b =
C. a = b·tanA,b = c·sinA D. a = ,b =
1.某人上坡走了75米,垂直距离上升了45米,则这个坡的坡度为( );
A.36°52′ B.30°58′ C.3︰5 D.3︰4
2. 如图1-7,某风景区改造中,需测量湖两岸游船码头A、B间的距离,设计人员由码头A沿与AB垂直的方向前进500米到达C处,测得∠ACB = 65°30′,则两码头间的距离
如图1-7,某风景区改造中,需测量湖两岸游船码头A、B间的距离,设计人员由码头A沿与AB垂直的方向前进500米到达C处,测得∠ACB = 65°30′,则两码头间的距离
AB约为 (精确到1米).
1.如图1-6,工厂车间的屋顶人字架是一个等腰三角形,AB = AC,BC = 15米,∠BAC = 100°. 则中柱AD = ,上弦AB = (精确到0.1米);
3. 三角函数的有关计算
练习一
[基础练习]一、1. 0.6198,0.4163,0.09101;2. 1.917;3. 30°55′02″,67°29′12″. 二、1. D; 2. C. 三、1.(1)41.54;(2)1.303;(3)1.270;(4)0.2929. 2.(1)35°16′;(2)73°24′;(3)28°;(4)24°41′.
[综合练习]∠ACB = 65°54′.
[探究练习] 原式 = 1,规律:tanα·tan (90°-α) = 1(α为锐角).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com