
1.借助计算器,解决含三角函数的实际问题,提高用现代工具解决实际问题的能力.
3.能够运用计算器辅助解决含三角函数值计算的实际问题.
2.能够用计算器进行有关三角函数值的计算.
1.经历用计算器由已知锐角求三角函数值的过程.进一步体会三角函数的意义.
3.需要知道角,而角又不易测量的实际问题.
例1(V形槽)
例2(放射性治疗肿瘤)
2.熟练掌握用科学计算器由已知三角函数值求出相应的锐角.
例如:sinA=0.9816.∠A= .
cosA=0.8607,∠A= ;
tanA=0.1890,∠A= ;
tanA=56.78,∠A= .
1.提出问题:如何由已知三角函数值,求相应的锐角.例如:sinA=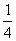 ,那么∠A是多少度呢?
,那么∠A是多少度呢?
1.已知sinθ=0.82904.求∠θ的大小.
解:∠θ≈56°1″
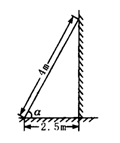 2.一梯子斜靠在一面墙上.已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成的锐角.
2.一梯子斜靠在一面墙上.已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成的锐角.
解:如图.cosα=
=0.625,α≈51°19′4″.
所以梯子.与地面所成的
锐角约51°19′4″.
Ⅳ.课时小结
本节课我们学习了用计算器由三角函数值求相应的锐角的过程,进一步体会三角函数的意义.并且用计算器辅助解决含有三角函数值计算的实际问题.
Ⅴ.课后作业
习题1.5第1、2、3题
Ⅵ.活动与探究
如图,美国侦察机B飞抵我国近海搞侦察活动,我战斗机A奋起拦截,地面雷达C测得:当两机都处在雷达的正东方向,且在同一高度时,它们的仰角分别为∠DCA=16°,∠DCB=
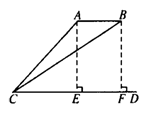 15°,它们与雷达的距离分别为AC=80千米,BC=81千米时,求此时两机的距离是多少千米?(精确到0.01千米)
15°,它们与雷达的距离分别为AC=80千米,BC=81千米时,求此时两机的距离是多少千米?(精确到0.01千米)
[过程]当从低处
观测高处的目标时.视
线与水平线所成的锐
角称为仰角.两机的距
离即AB的长度.根据
题意,过A、B分别作AE⊥CD,BF⊥CD.E、F为垂足,所以AB=EF,而求EF需分别在Rt△AEC和Rt△BFC中求了CE、CF,则EF=CF-CE.
[结果]作AE⊥CD,BF⊥CD,E、F为垂足,
∴cos16°=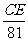 ,∴CE=80×cos16°≈80×0.96=76.80(千米).
,∴CE=80×cos16°≈80×0.96=76.80(千米).
∴cos15°=  ,∴CF=81×cos15°≈81×0.97=78.57(千米).
,∴CF=81×cos15°≈81×0.97=78.57(千米).
依题意AB=EF=CF-CE=79.57-76.80=1.77(千米).
所以此时两机的距离为1.77千米.
板书设计
§3.3.2 三角函数的有关计算(二)
3.解直角三角形
[师]我们讨论锐角三角形函数,都是将锐角放到直角三角形中讨论,又一次揭示了直角三角形中的边角关系.你知道在直角三角形中,除直角外,有几个元素组成?
[生]5个元素,两个锐角,两条直角边和一条斜边.
[师]根据我们所学知识,你知道这些边、角有什么样的关系吗?请同学们有条理地思考并回答.
[生]在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c.
(1)边的关系:a2+b2=c2(勾股定理);
(2)角的关系:∠A+∠B=90°;
(3)边角关系:sinA=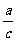 ,cosA=
,cosA= ,tanA=
,tanA=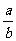 ;sinB=
;sinB= ,cosB=
,cosB=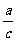 ,tanB=
,tanB=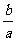 .
.
[师]由前面的两个例题以及上节的内容我们町以发现,很多实际问题中的数量关系都可归结为直角三角形中元素之间的关系,使实际问题都得到解决.
Ⅲ.随堂练习
2.运用计算器辅助解决含三角函数值计
算的实际问题.
 多媒体演示
多媒体演示
[例1]如图,工件上有
-V形槽.测得它的上口
宽加20 mm深19.2mm。求
V形角(∠ACB)的大
小.(结果精确到1°)
分析:根据题意,可知AB=20 mm,CD⊥AB,AC=BC,CD=19.2 mm,要求∠ACB,只需求出∠ACD(或∠DCB)即可.
解:tanACD= ≈0.5208,
≈0.5208,
 ∴∠ACD=27.5°,
∴∠ACD=27.5°,
∠ACB=2∠ACD≈2×27.5°=55°.
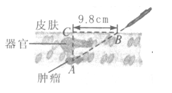
[例2]如图,一名
患者体内某重要
器官后面有一肿
瘤.在接受放射性
治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必须从侧面照射肿瘤.已知肿瘤在皮下6.3 cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求射线的入射角度,
解:如图,在Rt△ABC中,
AC=6.3 cm,BC=9.8 cm,
∴tanB= ≈0.6429.
≈0.6429.
∴∠B≈32°44′13″.
因此,射线的入射角度约为32°44′13″.
注:这两例都是实际应用问题,确实需要知道角度,而且角度又不易测量,这时我们根
据直角三角形边的关系.即可用计算器计算出角度,用以解决实际问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com