
7、已知:如图,□ABCD中,BD是对角线,AE⊥BD于E,CF⊥BD于F.
 求证:BE=DF.
求证:BE=DF.
6、平行四边形ABCD的两条对角线AC与BD相交于O,已知AB=8,BC=6,
△AOB的周长为18,求△AOD的周长。
1.(A)1 (B)2 (C) (D)1.5
5如图,四边形ABCD是平行四边形,对角线AC、BD相交
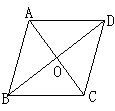 于点O,边AB可以看成由_____________平移得来的,△ABC可以看成由__________绕点O旋转______________得来;
于点O,边AB可以看成由_____________平移得来的,△ABC可以看成由__________绕点O旋转______________得来;
4.延长平形四边形ABCD的一边AB到E,使BE=BD,连结DE交BC于F,
若∠DAB=120°,∠CFE=135°,AB=1,则AC 的长为( )
3.在 中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是 ( )
中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是 ( )
A. 5 B. 10 C. 15 D. 20
2.已知□ABCD中,AB=8,BC=10,∠B=45°, □ABCD的面积为_________.
1.□ABCD的周长为50cm,且AB: BC = 3:2,则AB=______cm,BC=______cm.;
活动1、上表中平行四边形的性质中,你能证明哪些性质?
活动2、你认为平行四边形性质中,可以先证明哪一个?为什么?
活动3、证明定理“平行四边形对角线互相平分”。
由此证明过程,同时也证明了定理“平行四边形对边相等”、“平行四边形对角相等”,这样我们可得平行四边形的三条性质定理:
平行四边形对边相等。
平行四边形对角相等。
平行四边形对角线互相平分。
例1 :已知:如图,□ ABCD中,E、F分别是AD、BC的中点。
求证:BE=DF
分析:可根据证明△ABE≌△CDF得到结论。
若将例1中的“E、F分别是AD、BC的中点”改为“AE=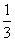 AD,CF=
AD,CF=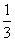 BC”,是否还能得到同样的结论?
BC”,是否还能得到同样的结论?
练习:P15 1、2
例2、 证明“夹在两条平行线之间的平行线段相等”
分析:根据命题先画出相应图形,再由命题与所画图形写出已知、求证,最后根据已知条件写出证明过程。
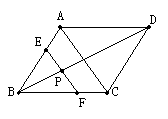
例3(广东省)如图,四边形ABCD是平行四边形,点F在BA的延长线上,连结CF交于AD点E.
求证:(1)△CDE∽△FAE
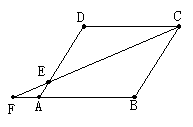 (2)当E是AD的中点,且BC=2CD时,求证:∠F=∠BCF
(2)当E是AD的中点,且BC=2CD时,求证:∠F=∠BCF
证明: (1)∵四边形ABCD为平行四边形
∴AB ∥CD,
∴∠D=∠EAF
∵∠DEC=∠AEF,
∴△CDE∽△FAE
(2)∵△CDE∽△FAE
∴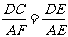
∵E是AD的中点
 ∴AF=DC
∴AF=DC
∵AD=BC, BC=2CD
∴AD=2AF
∴AE=AF
∴∠F=∠AEF
∵AD∥CB,
∴∠AEF=∠BCF
∴∠F=∠BCF
说明 平行四边形能带来平行线、等角,从而为得到比例线段、相似三角形创造了条件,也就为利用相似解决问题带来了方便.
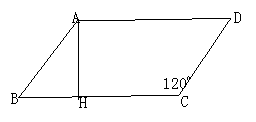 练习:1、已知:如图,在平行四边形ABCD中,AB=8cm,
练习:1、已知:如图,在平行四边形ABCD中,AB=8cm,
BC=10cm,∠C=1200,
求BC边上的高AH的长;
求平行四边形ABCD的面积
2、如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是( B )
A.6 B.8 C.9 D.10
根据我们曾经探索得到的平行四边形、矩形、菱形、正方形的性质,填写下表:
|
|
平行四边形 |
矩形 |
菱形 |
正方形 |
|
对边平行 |
|
|
|
|
|
对边相等 |
|
|
|
|
|
四边相等 |
|
|
|
|
|
对角相等 |
|
|
|
|
|
4个角是直角 |
|
|
|
|
|
对角线互相平分 |
|
|
|
|
|
对角线相等 |
|
|
|
|
|
对角线互相垂直 |
|
|
|
|
|
两条对角线平分两组对角 |
|
|
|
|
从上面的几种特殊四边形的性质中,你能说说它们之间有什么联系与区别吗?
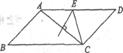
如图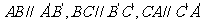 ,图中有______个平行四边形。
,图中有______个平行四边形。
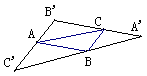
8.已知:如图,在菱形ABCD中,点E,F分别在CD,BC上,且CE=CF,求证:AE=AF.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com