
2、如图,已知菱形的两条对角线长为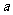 ,
,
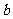 ,你能将菱形沿对角线分割后拼接成矩形吗?画图说明
,你能将菱形沿对角线分割后拼接成矩形吗?画图说明
(拼出一种图形即可);在此过程中,你能发现菱形的面
积与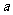 ,
,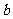 的关系吗?
的关系吗?
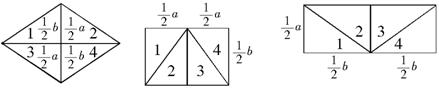 拼法(1) 拼法(2)
拼法(1) 拼法(2)
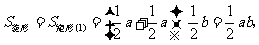 或
或 结论:菱形的面积等于两对角线乘积的一半.
结论:菱形的面积等于两对角线乘积的一半.
问题一 观察平行四边形和菱形的对角线把它们所分成的三角形,你有何发现?(引导学生不断地学会从多个角度观察、认识图形,主动地发现和获得新的数学结论,不断地积累数学活动的经验)
问题二 证明:菱形的4条边都相等。
菱形的对角线互相垂直,并且每一条对角线平分一组对角。
分析:第一条定理可先用“两组对边分别相等”证明平行四边形,再利用一组邻边相等得证;第二条定理可利用“三线合一”证得。
问题三 已知菱形的两条对角线长分别为6和8,由此你能获得有关这个菱形的哪些结论?(可得到边长为5;面积为24)你认为菱形的面积与菱形的两条对角线的长有关吗?如果有关,怎样根据菱形的对角线的计算它的面积?
由此可得:菱形的面积等于它的两条对角线长的积的面积。
 例 1、 如图3个全等的菱形构成的活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间 的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间 的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
例 1、 如图3个全等的菱形构成的活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间 的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间 的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?

分析:可将问题归结到菱形ABCD中研究,求出BD的长即可。可根据菱形的对角线互相垂直平分利用勾股定理求出BD。
练习P18 1、2
例2 已知:如图,四边形ABCD是菱形,G是AB上任一点,
 DF交AC于点E。
DF交AC于点E。
求证:∠AGD=∠CBE
分析:结合“全等三角形对应角相等”和“两直线平行,内错角相等”即可得证。
练习:
1、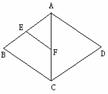 如图,在菱形ABCD中,E、F分别是AB、CD的中点,
如图,在菱形ABCD中,E、F分别是AB、CD的中点,
如果EF=2,那么ABCD的周长是( D )
A.4 B.8
C.12 D.16
4.请你折-折,观察并填空。(引导学生归纳。)
(1)菱形是不是中心对称图形?对称中心是_______。
(2)是不是轴对称图形?对称轴有几条?_______。
3.概括。
菱形特征1:菱形的四条边都相等。
菱形特征2:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角。
引导学生剖析矩形与菱形的区别。
矩形的对边平行且相等,四个角都是直角,对角线相等且互相平分;菱形的四条边都相等,对边平行,对角相等,对角线互相垂直平分,每条对角线平分它的一组对角。
2.探索。
请你作该菱形的对角线,探索菱形有哪些特征,并填空。
(从边、对角线入手。)
(1)边:都相等; (2)对角线:互相垂直。
(学生通过自己的操作、观察、猜想,完全可以得出菱形的特征,这对学生来说是富有意义的活动,学生对此也很感兴趣。)
问题:你怎样发现的?又是怎样验证的?
(可以指名学生到讲台上讲解一下他的结果。)
1. 将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形? (同桌互相帮助。)
将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形? (同桌互相帮助。)
2、菱形的判定方法。
1、用直尺和圆规作一个菱形,并说明作图依据。
5、将一张长方形纸片既快又准确地剪出一个菱形,并说出这样剪的依据。
4、已知:如图,□ABCD的对角线AC的垂直平分线与边AD、BC
分别相交于点E、F。
求证:四边形AFCE是菱形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com