
2、一个图形的形状越特殊,它的判定需要的条件就越多。
1、特殊的图形具有一般图形的性质和它的特殊性质。
5、如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成( C )
 A.
A. 角 B.
角 B.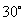 角
角
C.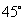 角 D.
角 D. 角
角
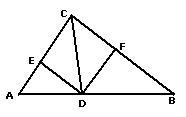
3、已知:如图,在Rt△ABC中,∠ACB=90°,
 CD是角平分线,DE⊥AC,DF⊥BC,垂足分别为E、F。
CD是角平分线,DE⊥AC,DF⊥BC,垂足分别为E、F。
求证:四边形ECFD是正方形。
2、如图,△ABC中,∠ACB=90°,CD平分∠ACB,
DE⊥AC,DF⊥BC,E、F是垂足。
求证:四边形DECF是正方形。
1、(2006·深圳市)如图6所示,在四边形ABCD中,
AB=BC=CD=DA,对角线AC与BD相交于点O.若不
增加任何字母与辅助线,要使得四边形ABCD是正方形,
则还需增加的一个条件是 .AC=BD
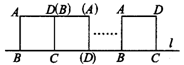
2、(2006年黄冈市)如图2,将边长为8cm的正方形ABCD的四边沿直线L向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是________cm.
为了活跃学生思维,可以提出以下问题:
①对角线相等的菱形是正方形吗?为什么?
②对角线互相垂直的矩形是正方形吗?为什么?
③对角线垂直且相等的四边形是正方形吗?为什么?
④四条边都相等的四边形是正方形吗?为什么?
⑤说“四个角相等的四边形是正方形”对吗?
判定方法
(1)矩形、菱形法:先判定四边形是矩形,再判定这个矩形是菱形(一组邻边相等的矩形);或者先判定四边形是菱形,再判定这个菱形也是矩形(有一个角是直角的菱形)。
(2)定义法:有一组邻边相等且有一个角是直角的平行四边形是正方形,这是直接利用定义来判定的。
如何用直尺和圆规作正方形?如何把长方形纸片通过折纸,剪出一个正方形纸片?
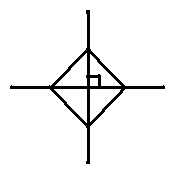


例1 已知:如图,E、F、G、H分别是正方形各边的中点,
AF、BG、CH、DE分别两两相交于点A’、B’、C’、D’。
求证:四边形是正方形。
分析:如右图,正方形ABCD中,点F、G分别是BC、CD
 的中点,AF、BG相交于点P,AF与BG互相垂直吗?若将点F、
的中点,AF、BG相交于点P,AF与BG互相垂直吗?若将点F、
G分别是BC、CD的中点改为BF=CG,是否有同样的结论?
同上,本例可考虑证“有一组邻边相等的矩形是正方形”。
(是否还有其他证明方法?与同学交流)
若点E、F、G、H分别在正方形ABCD的各边上,且
AE=BF=CG=DH,则四边形A’B’C’D’还是正方形吗?证明你的结论。
练习:1、P25 练习1、2

例2:已知:如图,点A'、B'、C'、D'分别是正方形ABCD
四条边上的点,并且AA'=BB'=CC'=DD'。
求证:四边形A‘B’C‘D’是正方形
例3、如图,在Rt△ABC与 Rt△ABD中,∠ABC=∠BAD=90°,AD=BC,AC,BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA 交DA的延长线于点F,AE,BF相交于点H.
(1)图中有若干对三角形是全等的,请你任选一对进行证明;(不添加任何辅助线)
(2)证明四边形AHBG是菱形;
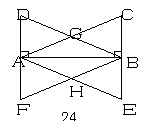 (3)若使四边形AHBG是正方形,还需在Rt△ABC 的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)
(3)若使四边形AHBG是正方形,还需在Rt△ABC 的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)
练习:
1.用两个全等的直角三角形拼下列图形:①平行四边形;②矩形;③菱形;④正方形;⑤等腰三角形;⑥等边三角形;一定可以拼成的是________(只填序号).
正方形是特殊的矩形和特殊的菱形,那么什么样的矩形是正方形?什么样的菱形是正方形?
(1)
 正方形与矩形,菱形,平行四边形的关系如下图。
正方形与矩形,菱形,平行四边形的关系如下图。
(2)正方形的性质:
①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形既是轴对称图形,又是中心对称图形。
⑤正方形对角线相等,互相垂直平分,每条对角线平分一组对
(3)本节课我们把探索和解决问题的思路、方法、结论,从特殊情形逐步推广到一般的情形,从而得到一般的结论,这也是我们获得数学结论的一种重要的思想方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com