
6、(2006·济南市)现有若干张边长不相等但都大于4cm的正方形纸片,从中任选一张,如图从距离正方形的四个顶点2cm处,沿45°角画线,将正方形纸片分成5部分,则中间阴影部分的面积是 8; cm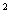 ;若在上述正方形纸片中再任选一张重复上述过程,并计算阴影部分的面积,你能发现什么规律?
.得到的阴影部分的面积是
;若在上述正方形纸片中再任选一张重复上述过程,并计算阴影部分的面积,你能发现什么规律?
.得到的阴影部分的面积是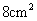 ,即阴影部分的面积不变.
,即阴影部分的面积不变.

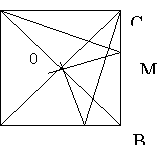
5、如图,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由.
|
N |

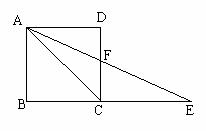
4、如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:(1)∠E=22.50. (2) ∠AFC=112.50. (3) ∠ACE=1350(4)AC=CE(5) AD∶CE=1∶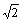 . 其中正确的有( )(A)5个 (B)4个 (C)3个 (D)2个
. 其中正确的有( )(A)5个 (B)4个 (C)3个 (D)2个
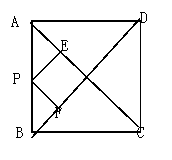
3、如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF= 。可以用一句话概括:正方形边上的任意一点到两对角线的距离之和等于
。
2、如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于E,交CD于F, 则∠BEC= 度.
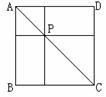
1、如图,正方形ABCD中,AB=1,点P是对角线AC上的一点,分别以AP、PC为对角线作正方形,则两个小正方形的周长的和是_________。

2、已知:如图,正方形ABCD的周长为4a,四边形EFGH四个顶点E、F、G、H分别在AB、BC、CD、DA上滑动,在滑动过程中,始终有EH∥BD∥FG,且EH=FG,那么四边形EFGH的周长是否可求?若能求出,它的周长是多少?若不能求出,请说明理由.
探索正方形的性质
(1)边的性质: ;
(2)角的性质: ;
(3)对角线的性质: ;
(4)对称性: 。
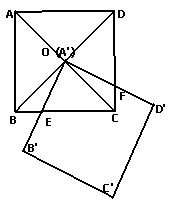
例1、 已知:如图,正方形ABCD的对角线AC、BD相交于
点O;正方形A’B’C’D’的顶点A’与点O重合,A’B’交BC于点E,
A’D’交CD于点F,E是BC的中点。

(1)求证:F是CD的中点
(2)若正方形A’B’C’D’绕点O旋转某个角度后,OE=OF吗?
 分析:(1)方法一∵OB=OC,E是BC的中点
分析:(1)方法一∵OB=OC,E是BC的中点
∴OE⊥BC,∠OEC=90°
∵∠EA’F=∠ECF=90°
∴∠OFC=90°
∵OC=OD
∴F是CD的中点
方法二 ∵∠EA’F=90°,AC⊥BD ∴∠EOC+∠COF=∠DOF+∠COF=90°
∴∠EOC=∠DOF 又OC=OD,∠OCE=∠ODF=45°
∴△OCE≌△ODF(ASA)
∴DF=CE=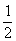 BC=
BC=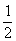 CD,即F是CD的中点。
CD,即F是CD的中点。
(2)证明方法同前方法二。
由(1)、(2)可以得到什么结论?(无论正方形A’B’C’D’绕点O旋转并与正方形ABCD分别交BC、CD于点E、F,总有OE=OF,BE=CF,EC=FD,两个正方形的重叠部分的面积始终等于正方形ABCD面积的四分之一等等)
练习
 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( C )
如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( C )
A.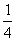 cm2 B.
cm2 B.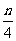 cm2
C.
cm2
C.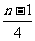 cm2
D.
cm2
D.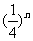 cm2
cm2
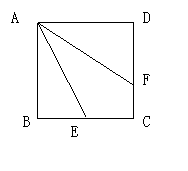
 例2、已知,在正方形ABCD中,E是BC的中点,点F在CD上,∠FAE﹦∠BAE.
例2、已知,在正方形ABCD中,E是BC的中点,点F在CD上,∠FAE﹦∠BAE.
求证:AF﹦BC+FC.
例3、 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
例4、已知正方形ABCD。
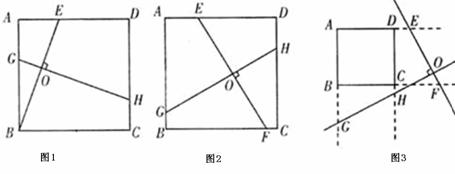
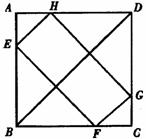
(1)如图1,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H,求证:BE=GH;
(2)如图2,过正方形ABCD内任意一点作两条互相垂直的直线,分别交AD、BC于点E、F,交AB、CD于点G、H,EF与GH相等吗?请写出你的结论;
(3)当点O在正方形ABCD的边上或外部时,过点O作两条互相垂直的直线,被正方形相对的两边(或它们的延长线)截得的两条线段还相等吗?其中一种情形如图3所示,过正方形ABCD外一点O作互相垂直的两条直线m、n,m与AD、BC的延长线分别交于点E、F,n与AB、DC的延长线分别交于点G、H,试就该图对你的结论加以证明。
练习:
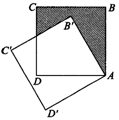
1、(2006年潍坊市)如图7,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
A.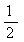 B.
B.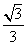 C.1-
C.1-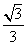 D.1-
D.1-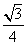
这是一个流传在世界各地的故事,三姐妹的父亲是一位慈祥的阿拉伯老人。一天,老人不幸去世,临终,老人留给三个女儿一件珍贵的传家宝--一块五色斑斓的正方形地毯,深爱父亲的女儿们都想得这块地毯,以作纪念。大姐想出了一个好办法:“把它裁成三个小正方形地毯,为了不使地毯剪得过于零碎,最好只剪成4块,其中两块是正方形,另外两块可以拼成一个正方形。”聪明的你能想出一个巧妙的剪法,符合大姐的设想吗?
进行推理论证常常需要从两个方向思考:“证明结论,需要什么条件?”“从已知条件可以推出哪些证明结论所需的事项?”这样有利于探索并获得证明的思路。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com