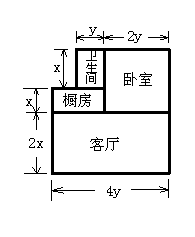
6．矩形两条对角线的夹角为60°，一条对角线与短边的和为15cm，则矩形较短边长为(　 )

　 A．4cm　　 B．2cm　　 C．3cm　　 D．5cm

5．菱形的两条对角线长分别为3和4，那么这个菱形的面积为(平方单位)(　 )．

　 A．12　　　 B．6　　　 C．5　　 D．7

4．在正方形ABCD所在的平面上，到正方形三边所在直线距离相等的点有(　 )．

　 A．3个　　 B．4个　　 C．5个　　　 D．6个

3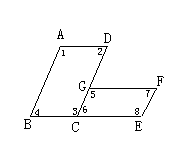．如图所示，四边形ABCD和CEFG都是平行四边形，　 下面等式中错误的是(　 )．

　 A．∠1+∠8=180⁰;　 B．∠2+∠8=180°;

C．∠4+∠6=180°;　 D．∠1+∠5=180°

2．下列命题中正确的是(　 )．

　 A．对角线互相垂直的四边形是菱形;　　　 B．对角线相等的四边形是矩形

　 C．对角线相等且互相垂直的四边形是菱形;D．对角线相等的平行四边形是矩形

1．下面几组条件中，能判定一个四边形是平行四边形的是(　 )．

　 A．一组对边相等;　　 B．两条对角线互相平分

　 C．一组对边平行;　　 D．两条对角线互相垂直

1．平行四边形的证明

定理 一组对边平行且相等的四边形是平行四边形

已知：在四边ABCD形中，AB∥CD，AB=CD

求证：四边ABCD是平行四边形。

　

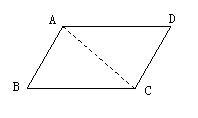
　　　　　　　 思考与表达

怎么想　　　　　　　　　　 怎么写

　　　 要证四边形ABCD是平行四边形

　　　 已知ABCD，因而

　　　 只需证BC∥AD

　　　 连接AC

　　　 只需证∠ACB=∠CAD

　　　 只需证△ABC≌△CDA

定理: 对角线互相平分的四边形是平行四边形

　
　
学生填空
　
　
　
　
　
　
　
　
　
学生分析命题画出图形写出已知求证
　
　
　
　
　
　
　
　
　
　
学生根据推理过程写出证明过程
　
　
　
　
　
学生讨论运用
什么方法证明
　
　
　
　
学生能够准确熟练的将文字语言转化为符号语言
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
学生能够比较想与写的过程的互逆性,避免书写过程中两者发生混淆.
　
运用不同的方法体现选择发的重要性

教师活动内容、方式	学生活动方式	设计意图
拓展延伸:如果OA=OC,OB＜OD,那么四边形ABCD不是平行四边形 这个结论成立吗?如果成立,你能证明吗? 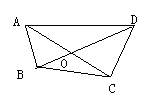假设四边形ABCD是平行 四边形,那么OA=OC,OB=OD, 这与条件OB＜OD矛盾， 所以四边形ABCD不是 平行四边形。 　 结论：这种不是从已知条件出发直接证明命题的结论成立，而是提出了与矛盾相反的假设，然后由这个“假设”出发推导出了矛盾的结果，从而证明了命题的结论一定成立。 例题：已知平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F，求证：四边形AECF是平行四边形 　　　　 A　　　　 B 　　　　　　　　　 E 　 F D　　　 C 教师引导学生分析，找出证明平行四边形的方法 四. 课堂巩固 课本P20T1、2 五．小结 　 1 回顾情境创设中问题是如何解决的？ 　2．谈谈学习这课的感受？ 六．作业 课本P25T1、2	学生讨论，引导学生如何寻找证明思路 　 　 　 　 　 　 　 　 　 　 　 　 学生思考证明思路	反证法学生刚刚接触，还不太熟悉还需多多引导 　 　 　 　 　 　 　 　 　 　 巩固平行四边形的判定方法，一题多解拓展学生思维

3、今天，让我们一起，用基本事实和学过的定理来证明平行四边形的性质。

时间较长，学生有点遗忘，可让学生分组讨论后再回答
　
　
　
　
　
　
　
让学生回答，相互补充完整。
复习旧知识，为这一节课讲授平行四边形性质作铺垫。
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
提出本节课的学习目标。
　
　
教师活动内容、方式
学生活动方式
设计意图
二、探讨活动
1、(师生共同探讨)已知如图在□ABCD中，AC、DB相交于点O求证：AO=CO，BO=DO。
思考与表达
怎　　 要证AO=CO，BO=DO，　　 怎
么　　 只需证△AOB≌△COD,　 　　　么
想　　 只需证AB=CD，　　　　　　 写
只需证△ABC≌△CDA，
2、学生独立思考
利用上面的证明过程，你还能证明平行四边形的其他性质吗？
三、归纳。
定理：平行四边形的对边相等。
定理：平行四边形的对角相等。
定理：平行四边形的对角线互相平分。
四、例题教学
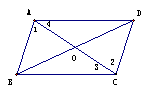例：已知如图，在□ABCD中，E、F分别是AD、BC的中点，求证：BE=DF。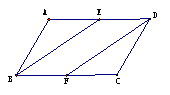
思考与表达
怎　　 要证BE=DF，　　　　　　　 怎
么　　 只需证△ABE≌△CDF,　　　 么
想　　 只需证AB=CD，AE=CF，　　 写
∠A=∠C。
拓展延伸　 如果连接AF、CE，有哪些结论？
五、课堂小结：
通过本节课的学习，你有哪些收获，你能与同学们交流吗？
六、课堂练习：P15第1-2题。
七、布置作业；P25习题1-3题，第1-2题。
　
　
　
　
　
　
学生思考回答，重点要求说明是怎样想的。
　
　
　
　
　
　
　
　
　
　
　
学生分析思路：怎样想。
　
　
　
　
　
　
学生归纳总结
　
要重视怎样想的分析：
几何推理要教会学生分析的方法。
　
　
进一步培养学生分析问题的能力。
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
培养学生归纳的能力和表达的能力。
　

　　　　　　　

2、你能说说这几种特殊四边形的性质之间有哪些区别和联系吗？

(1)　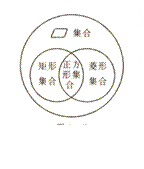　 正方形与矩形，菱形，平行四边形的关系如下图。

(2)正方形的性质：

①正方形对边平行。

②正方形四边相等。

③正方形四个角都是直角。

④正方形既是轴对称图形，又是中心对称图形。

⑤正方形对角线相等，互相垂直平分，每条对角线平分一组对

(3)本节课我们把探索和解决问题的思路、方法、结论，从特殊情形逐步推广到一般的情形，从而得到一般的结论，这也是我们获得数学结论的一种重要的思想方法。