
1.3线段的垂直平分线(第一课时)
教学目标:
本节课从学生熟知的诗词引入,以及就地取材--我校门口有几个养鸭池而设计“统计鸭子数量增减”这个问题。利用这些教学资源制作课件,学生刚看到这些熟悉的画面,情绪很高,兴趣也很浓。通过实践,我觉得本节课较好地体现了《新课标》提出的任务型教学(学中用,用中学);学生主体地位明显、突出;学生在轻松、快乐的课堂中,较好地完成了本节的学习任务。
|
问题与情景 |
师生互动 |
设计意图 |
|
|||
|
一、复习导入 课件显示: 1、我国北方漂亮的雪景(背景配音:毛泽东的《沁园春·雪》:北国风光,千里冰封,万里雪飘……)。 2、问题:象局预报: (1) 延安2007年2月3日6点气温为 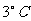 ,当天最高气温比6点的气温高出 ,当天最高气温比6点的气温高出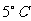 ,当天最高气温多少度?怎么计算? ,当天最高气温多少度?怎么计算?(2) 延安2007年2月6日2点气温为 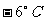 ,当天最高气温比2点的气温高出 ,当天最高气温比2点的气温高出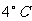 ,当天最高气温多少度?怎么计算? ,当天最高气温多少度?怎么计算?课件出示课题 |
教师:零下3摄氏度可记为 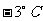 ,7摄氏度可记为 ,7摄氏度可记为 ,零下10摄氏度可记为 ,零下10摄氏度可记为 。-3、7、-10的绝对值分别是什么?它们的相反数又是多少呢? 。-3、7、-10的绝对值分别是什么?它们的相反数又是多少呢?学生的回答: ①:-3的相反数是3,7的相反数是-7,-10的相反数是10 ②:-3的绝对值是3,7的绝对值是7,-10的绝对值是10 问题(1):学生回答:3+5=8 当天最高气温是 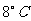 问题(2)有学生能列出式子:(-6)+4,但不会计算。 教师结合式子(-6)+4引出课题。 类似的有理数的加法怎么计算呢?这就是我们这节课探讨的问题--有理数的加法。 (教师板书课题) |
从学生熟知的诗词《沁园春·雪》开始。一下子就调动了学生的学习积极性。进而开始本课的教学。 先复习有理数的绝对值和相反数,承上巩固前面的知识,并用于本节课的教学。 通过这个问题引导学生积极思考,激发学生探究新知的兴趣。 |
|
|||
|
二、讲授新课 (播放动画。背景音乐为儿歌《数鸭子》:“门前大桥下,游过一群鸭,快来快来数一数,二四六七八……”)画面上一个十三、四岁的男孩站在一个池塘边,许多鸭子正在池塘中畅游。画外音:小明的爸爸是农民,在自家的鱼塘养鸭。又到了收成的季节,每天都有人来买鸭,又不时地买进小鸭子。小明是一个懂事的孩子,暑假抓紧完成作业后,就去帮爸爸的忙。还专门对某一周七天鸭子的买卖做了如下统计: |
老师:同学们,我们规定:买进(增加)为正;卖出(减少)为负;如果买进30只鸭子记为+30只鸭子,卖出20只鸭子记为-20只鸭子,请你们帮小明统计一下这一周每天鸭子数量的增减情况。并用数学式子表示出来。 小组内讨论后派代表发言。 |
这个问题比书本上,“一个物体作左右运动”,更贴近农村学生的生活,学生也更熟悉。学生的学习兴趣更高。问题提出来以后,学生的学习积极性一下就调动起来了。引导学生积极思考,做好热身运动。 |
|
|||
|
问题与情景 |
师生互动 |
设计意图 |
|
|||
|
(1)星期一:上午买进80只鸭子, 下午买进60只鸭子; (2)星期二:上午卖出20只鸭子, 下午卖出30只鸭子; (3)星期三:上午买进80只鸭子, 下午卖出25只鸭子; |
学生:星期一小明家增加了140只鸭子,用式子表示为: +140 =(+80)+(+60)教师:大家对这个式子有什么看法? 学生: 140只鸭子是上午60只鸭子和下午的80只鸭子的和,写在这个式子的右边比较合理。即: 80+60=140 …① 教师对学生的回答作点评,适当表扬,并提问:正数的正号能否省略? 根据学生回答画数轴。其中假设原点O为鸭子数量变化前的数量(图1)。 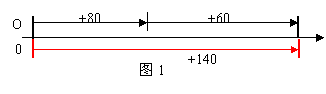 承上提问:(要求学生口答) (+12)+(+5)=? (+6)+1=? 5+(+6)=? 16+15=? 教师并归纳:有理数相加,正数的正号可以省略。 学生:星期二小明家减少50只鸭子,用式子表示为: (-20)+(-30)=-50…② 教师:这个运算用数轴表示如下(图2)。  承上提问:(要求学生口答) (-32)+(-15)=? (-6)+(-21)=? -5+(-6)=? -16+(-30)=? 提问:有理数相加,负数的负号能省略吗? 让学生明确:有理数相加,负数的负号不能省略。 学生:星期三小明家增加55只鸭子,用式子表示为:(+80)+(-25)=+55…③ 教师:这个运算用数轴表示如下(图3)。
|
教师对于这个式子,没直接纠正过来,而是让学生思考,发表看法,得出正确的书写形式。这样既培养了学生的判断能力,又提高了学生的思维能力。 通过数轴的分析使问题直观化(由在数轴上表示结果的点所处的位置,以及表示结果的点与原点的距离,就可确定变化后鸭子的数量。)并能实践我们所提倡的“数形结合”的数学思想 。 |
|
|||
|
问题与情景 |
师生互动 |
设计意图 |
|||||
|
(4)星期四:上午卖出45只鸭子, 下午买进30只鸭子; (5)星期五:上午买进30只鸭子, 下午卖出30只鸭子;假如只卖出40只鸭子,再买进40只鸭子,结果又怎样? (6)星期六:上午没买没卖,下午买进60只鸭子; (7)星期日:上午卖出20只鸭子,下午没买卖。 |
承上提问:(要求学生口答) (+32)+(-15)=? (+36)+(-21)=? -5+16=? 116+(-30)=? 学生:星期四小明家增加15只鸭子,用式子表示为: (-45)+(+30)=-15…④ 教师:这个运算用数轴表示如下(图4)。 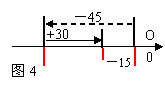 承上提问:(要求学生口答) 32+(-65)=? 12+(-21)=? -15+6=? 16+(-30)=? 学生:星期五小明家鸭子数量没变化,用式子表示为: 30+(-30)=0…⑤ (-40)+40=0 承上提问:(要求学生口答) 32+(-32)=? 16+(-16)=? -15+15=? 30+(-30)=? 学生:星期六小明家增加60只鸭子,用式子表示为: 0+60=+60…⑥ 承上提问:(要求学生口答) 32+(-32)=? 16+(-16)=? -15+15=? 30+(-30)=? 学生:星期天小明家减少了20只鸭子,用式子表示为: (-20)+ 0 =-20…⑦ 承上提问:(要求学生口答) 32+0=? 0+(-13)=? -18+0=? 20+0=? |
对各个问题分析后增加要求学生口答的问题,可初步强化有理数的加法运算,便于接下来加法法则的归纳总结。 |
|||||
|
三、合作交流,解读探究 课件出示刚才师生对话中的七个问题、七个式子和数轴,并出示问题:①你们还能举出不同以上七种情况的算式吗?②请同学们归纳一下,上面七个式子表示了几种不同的有理数相加? |
问题①: 生答:不能 教师:这说明这几个算式概括了有理数加法的不同情况。 问题②: 学生小组内讨论、交流,并回答: 有两个正数相加,两个负数相加,一正一负的两个有理数相加,0和一个有理数相加四种有理数相加。 |
根据学生回答的七个式子引导学生对有理数的加法法则概括和理解。 |
|||||
|
问题与情景 |
师生互动 |
设计意图 |
|
|||
|
课件出示问题:三类不同的有理数相加,怎样求它们的和呢(和的符号是怎样确定的?和的绝对值又是怎样确定的?)请同学思考回答并举例。 课件显示: 有理数加法法则: 1、同号两数相加,取相同符号,并把绝对值相加; 2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两数相加得0。 3、一个数同0相加,仍得这个数。 例如: (1)(-5 ) + (-9 ) (2)(-10 ) + (+ 3) |
师点评:这位同学的分法不错,同学们还有更好的分法吗? ……(学生继续回答) 教师适时对回答正确的给予表扬并概括如下: 分成3种: ①两个正数相加和两个负数相加就是同号两数相加; ②一正一负的两个有理数相加; ③0和一个有理数相加。 学生:同号两数相加,和的符号与加数的符号相同,并把绝对值相加; 如:(-6)+(-15)=-(6+15)=-21 学生:异号两数相加,和的符号与绝对值较大的加数的符号一样,并将两个绝对值相减。(较大-较小) 如:(-15)+(8)=-(15-8)=-7 学生:互为相反数的两个数的和为零; 如:(+1)+(-1) = 0; (+17) + (-17) = 0 教师对学生正确的回答给予肯定并总结有理数加法法则(课件显示) 教师强调:考虑有理数的运算结果时,要考虑它的符号,又要考虑它的绝对值。 例如(课件显示问题及解题过程,教师说明): (1)(-5 ) + (-9 ) = -(5 + 9) = -14 ↓ ↓ ↓ 同号两 取相 绝对值相加 数相加 同符号 (2)(-10 ) + (+ 3) = - ( 10 -3) = -7 ↓ ↓ ↓ 异号两 取绝对值较大 较大的绝对值减 数相加 的加数的符号 去较小的绝对值 教师再次强调:同号两数相加,绝对值是相加,而异号两数相加,绝对值应相减(较大的-较小的) |
培养学生的语言表达能力和归纳能力。也许学生说得不够严谨,但这并不重要,重要的是能用自己的语言表达自己所发现的规律。 强化理解总结步骤。特别强调本节教学重点--异号两数相加的情况。 |
|
|||
|
四、应用新知 1、例1计算: (1)(-3)+(-9) (2)(-4.7)+3.9 |
根据有理数加法法则,教师与学生一起完成例1。指定一学生回答,教师板演。 |
强调:要求学生在刚开始学的时 |
|
|||
|
问题与情景 |
师生互动 |
设计意图 |
|
||||
|
课件显示: 有理数加法解题步骤: (1)、先判断类型(同号或异号等); (2)、再确定和的符号; (3)、后进行绝对值的加减运算。 2、例2足球循环赛中,红队4:1胜黄队,黄队1:0胜蓝队,蓝队1:0胜红队,计算各队的净胜球数。 3、思考:在小学里,计算两个非零数相加时,它们的和总是大于其中任何一个加数,学习了有理数加法法则后,你认为这个结论还成立吗?请举例说明。 |
解:(1)-3+(-9)(同号两数相加) =-(3+9) (取相同的符号, =-12 并把绝对值相加)(2)(-4.7)+3.9 (异号两数相加) =-(4.7-3.9)(取绝对值较大的 =-0.9 加数的符号,并用 较大的绝对值减去较小的绝对值) 举一反三: 课件显示:将(1)式中的(-3)、(-9) 分别换成其它整数分别计算; 将(2)式中的(-4.7)和3.9分别换成其它正分数、负分数分别计算。 教师:什么叫净胜球数?请举例说明。 学生:足球比赛中,通常把进球数记为正数,失球数记为负数,它们的和就叫净胜球数。 比如:红队和蓝队进行了两场比赛,比分分别是1:0和0:2,那么红队的第一场进球数+1,第二场失球数是-2,所以红队的净胜球数是+1+(-2)= -1。 教师:回答正确!预习得不错。 教师巡视、指导。师生共同交流、完成。 学生在小组讨论后,得出: 两个有理数相加,和并不一定大于加数。并举例说明: (-3)+5=2 2<5 (-2)+(-6)=-8 -8<-2,-8<-6 |
候要把中间的过程写完整。 例1两小题分别是同号和异号两数相加。 “举一反三”目的是补充其它有理数加法的类型。 课前布置预习该题,特别是了解什么叫“净胜球数”的问题,为更好地讲解该题做好铺垫。 问题3的提出,是与小学学过的相关内容联系起来,进行观察、比较,从而发现规律,鼓励学生用自己的语言表达。 |
|
||||
|
五、小结 通过本节课的学习,你学到了哪些知识和方法?有什么感想? 学生回答后,教师做整理。 |
教师: 1、有理数加法运算法则 2、进行有理数加法运算的步骤为: (1)判断两个加数的符号,根据法则确定和的符号; (2)考虑两个加数的绝对值,根据法则确定和的绝对值。 |
通过表扬小结,鼓励学生继续努力,同时增强他们学习数学的自信心,使其在课堂上、生活中好地运用数学知识,做到“学以致用”。 |
|
||||
|
六、布置作业 课本24-25页习题1.3 第3题(1)-(4);第4题 |
学生课后完成,教师批改总结。 教师应关注:(1)不同层次的学生对知识的理解掌握程度并系统分析。 (2)对反馈的信息及时处理。 |
及时了解学生的学习效果,并据此调整教学安排。 |
|
||||
|
问题与情景 |
师生互动 |
设计意图 |
|
|||
|
七、拓展迁移 计算并思考(课件显示): (1)4+(-3) (2)(-3)+4 (3)(-12)+(-13) (4) (-13)+ (-12) (5)[(-5)+3]+(-3) (6) (-5)+[3+(-3)] |
教师:你能发现(1)和(2);(3)和(4);(5)和(6)三对式子之间的关系吗?这与我们小学学过的加法交换率、结合率有相同之处吗? 请同学们课后思考这个问题。 |
在掌握有理数加法法则的基础上,布置几道与《有理数运算律》有关的习题,目的是做好预习,为下节课的学习做好铺垫。 |
|
|||
2、课前准备:教师将北国风光图片、学校前面的养鸭池等作为素材并用于课件,方便新课的呈现。让学生从视觉感官上进一步感受新知识,以加深印象。
1、新课标提出“教师应该为学生营造一个轻松、和谐、愉快的学习氛围,使学生真正成为学习的主人。”结合本节的特点,我采取了“互动-交流”的教学模式,包括“师生互动、生生互动,以及师生与教材互动”三个方面,实行小组学习模式:将全班同学分成14组,每组4人,遇到讨论的问题组内先进行讨论,再派代表回答。不受拘束地表达自己对问题的想法,使学生真正成为课堂的主人,掌握一定的数学知识与技能,形成适合自己的学习策略。
海山三中是一所农村初级中学,多数学生的数学基础较差,学习方法不恰当。学生对新的课堂教学方法不是很适应;不过,在新的教学理念的指导下,旧的教学方法和学习方法已逐步淡化,学生的观察,比较,归纳及自主探索和合作交流能力已逐步形成。现在,班级中已初步形成合作交流、勇于探究、积极回答问题的良好学风,学生间互相评价和师生互动的课堂气氛也已逐步形成。
“有理数的加法”是人教版七年级数学上册第一章有理数的第三节内容,本节内容安排四个课时,本课时是本节内容的第一课时,本课设计主要是通过“统计鸭子数量的增减”的实例来明确有理数加法的意义,引入有理数加法的法则,为今后学习“有理数的减法”做铺垫。
6.难点
有理数加法中异号两数加法法则的运用。
5.重点
了解有理数加法的意义,会根据有理数加法法则进行有理数的加法运算。
4.情感与态度
认识到通过师生合作交流,学生主动参与小组讨论与探索获得数学知识,从而提高学生学习数学的积极性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com