1．经历探索、猜测、证明的过程，进一步发展学生的推理证明意识和能力．

2．能够利用尺规作已知线段的垂直平分线．

过程与方法目标：

1．经历探索、猜测过程，能够运用公理和所学过的定理证明线段垂直平分线的性质定理和判定定理．

3．线段的垂直平分钱(一)

知识与技能目标：

2、已知等腰三角形底边及底边上的高，你能用尺规作出等腰三角形吗？能作几个？(满足条件的等腰三角形可和出两个，分加位于已知边的两侧，它们全等)。

做一做：

已知底边上的高，求作等腰三角形。

已知：线段a、b

求作：△ABC，使AB=AC，且BC=a，高AD=h.

作法：

(1)作线段BC=a(如图)；　　　　　　 (2)作线段BC的垂直平分线L，交BC于点D，

(3)在L上作线段DA，使DA=h　　 (4)连接AB，AC。

△ABC为所求的等腰三角形。

作业：

教学后记：

3、能够利用尺规作已知线段的垂直平分线；已知底边及底边上的高，能利用尺规作出等腰三角形。

教学过程：

引入：

　 剪一个三角形纸片，通过折叠找出每条边的垂直平分线，观察这三条垂直平分线，你发现了什么？当利用尺规作出三角形三条边的垂直平分线时，你是否也发现了同样的结论？

定理：三角形三边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等。

证明：在△ABC中，设AB、BC的垂直平分线相交于点P，连接AP、BP、CP，

∵点P在线段AB的垂直平分线上

∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等)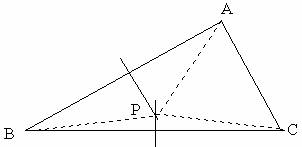

同理：PB=PC

∴PA=PC

∴点P在AC的垂直平分线上

(到一条线段两个端点距离相等的点，在这条线段的垂直平分线上)。

∴AB，BC，AC的垂直平分线相交于点P。

议一议：1、已知三角形的一条边及这条边上的高，你能作出三角形吗？如果能，能作几个？所作的三角形都全等吗？(这样的三角形能作出无数多个，它们不都全等)

2、作直线CD。

直线CD就是线段AB的垂直平分线。

请你说明CD为什么是AB的垂直平分线，

并与同伴进行交流。

因为直线CD与线段AB的交点就是AB的中点，

所以我们也用这种方法作线段的中点。

随堂练习：P26

作业：P27，1、2、3、

教学后记：

线段的垂直平分线(第二课时)

教学目标：

3、能够利用尺规作已知线段的垂直平分线；已知底边及底边上的高，能利用尺规作出等腰三角形。

教学过程：我们曾利用折纸的办法得到：线段垂直平分线上的点到这条线段两个端点的距离睛等，你能证明这一结论吗？

定理：线段垂直平分线上的点到这条线段两个端点的距离相等。

已知：如图，直线MN⊥AB，垂足是C，且AC=BC，P是MN上的任意一点。

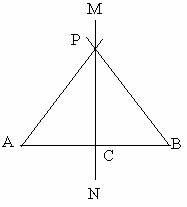求证：PA=PB。

证明：　　 ∵MN⊥AB，

∴∠PCA=∠PCB=90°

∵AC=BC，PC=PC

∴△PCA≌△PCB(SAS)

∴PA=PB(全等三角形的对应边相等)

想一想，你能写出上面这个定理的逆合题吗？

它是真命题吗？如果是请证明：

定理　 到一条线段两个端点距离相等的点，

在这条线段的垂直平分线上。

(利用等腰三角形三线合一)

做一做

用尺规作线段的垂直平分线

已知：线段AB

求作：线段AB的垂直平分线。

作法：1、分别以点A和B为圆心，

以大于AB的长为半径作弧，两弧相交于点C和D，

2、能够证明线段垂直平分线的性质定理、判定定理及其相关结论。

1、经历探索、猜测、证明的过程，进一步发展学生的推理证明意识和能力。