2、作直线CD。

直线CD就是线段AB的垂直平分线。

请你说明CD为什么是AB的垂直平分线，

并与同伴进行交流。

因为直线CD与线段AB的交点就是AB的中点，

所以我们也用这种方法作线段的中点。

随堂练习：P26

作业：P27，1、2、3、

教学后记：

3、能够利用尺规作已知线段的垂直平分线；已知底边及底边上的高，能利用尺规作出等腰三角形。

教学过程：我们曾利用折纸的办法得到：线段垂直平分线上的点到这条线段两个端点的距离睛等，你能证明这一结论吗？

定理：线段垂直平分线上的点到这条线段两个端点的距离相等。

已知：如图，直线MN⊥AB，垂足是C，且AC=BC，P是MN上的任意一点。

求证：PA=PB。

证明：　 ∵MN⊥AB，

∴∠PCA=∠PCB=90°

∵AC=BC，PC=PC

∴△PCA≌△PCB(SAS)

∴PA=PB(全等三角形的对应边相等)

想一想，你能写出上面这个定理的逆合题吗？

它是真命题吗？如果是请证明：

定理　 到一条线段两个端点距离相等的点，

在这条线段的垂直平分线上。

(利用等腰三角形三线合一)

做一做

用尺规作线段的垂直平分线

已知：线段AB

求作：线段AB的垂直平分线。

作法：1、分别以点A和B为圆心，

以大于AB的长为半径作弧，两弧相交于点C和D，

2、能够证明线段垂直平分线的性质定理、判定定理及其相关结论。

1、经历探索、猜测、证明的过程，进一步发展学生的推理证明意识和能力。

2、已知等腰三角形底边及底边上的高，你能用尺规作出等腰三角形吗？能作几个？(满足条件的等腰三角形可和出两个，分加位于已知边的两侧，它们全等)。

做一做：

已知底边上的高，求作等腰三角形。

已知：线段a、b

求作：△ABC，使AB=AC，且BC=a，高AD=h.

作法：

(1)作线段BC=a(如图)；　　　　 (2)作线段BC的垂直平分线L，交BC于点D，

(3)在L上作线段DA，使DA=h (4)连接AB，AC。

△ABC为所求的等腰三角形。

作业：

教学后记：

3、能够利用尺规作已知线段的垂直平分线；已知底边及底边上的高，能利用尺规作出等腰三角形。

教学过程：

引入：

　 剪一个三角形纸片，通过折叠找出每条边的垂直平分线，观察这三条垂直平分线，你发现了什么？当利用尺规作出三角形三条边的垂直平分线时，你是否也发现了同样的结论？

定理：三角形三边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等。

证明：在△ABC中，设AB、BC的垂直平分线相交于点P，连接AP、BP、CP，

∵点P在线段AB的垂直平分线上

∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等)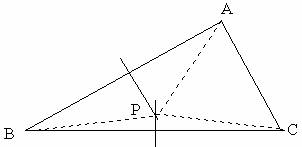

同理：PB=PC

∴PA=PC

∴点P在AC的垂直平分线上

(到一条线段两个端点距离相等的点，在这条线段的垂直平分线上)。

∴AB，BC，AC的垂直平分线相交于点P。

议一议：1、已知三角形的一条边及这条边上的高，你能作出三角形吗？如果能，能作几个？所作的三角形都全等吗？(这样的三角形能作出无数多个，它们不都全等)

2、能够证明线段垂直平分线的性质定理、判定定理及其相关结论。

1、经历探索、猜测、证明的过程，进一步发展学生的推理证明意识和能力。

2．已知等腰三角形的底边及底边上的高，你能用尺规作出等腰三角形吗？能作几个？

随堂练习：

随堂练习1、2

课堂小结：

本节课主要训练尺规作图，通过绘制图形，让学生体验定理在实际中的运用，感悟其实际价值。学习中要注意构思所要制作的图形的作法，画出草稿，分析方法。不要急于动手。对于三线一点的证明应总结其证明手法。在书写作法中，要注意几何语言的表达，同时注意作图的依据。

作业：

课本习题1．7　 1．2

1．的答案是：这样的三角形能作出无数个。它们不都全等。

议一议