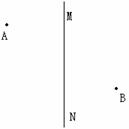
2.如图，在直线MN上求作一点P，使PA=PB。

补充题：

1.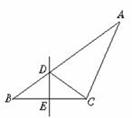如图，如果△ACD的周长为17 cm，△ABC的周长为25 cm，

根据这些条件，你可以求出哪条线段的长?

2. 补充题：见下页

1. 课本第21页习题1.4 　1、2、3

学生自己总结：

⑴ 线段是轴对称图形，线段的垂直平分线是它的对称轴。

⑵ 线段的垂直平分线上的点到线段两端的距离相等。　

⑶ 到线段两端距离相等的点，在这条线段的垂直平分线上。

⑷ 线段的垂直平分线是到线段两端距离相等的点的集合。

试一试：你能说明⑵⑶的理由吗？

活动二　 用圆规找点

问题1：已知线段AB, 你能用圆规找出一点Q，使AQ = BQ吗？说出你的方法并画出图形(保留作图痕迹)，你还能再找出符合上述条件的点M吗？(学生回答)

问题2：观察点Q、M，与直线l有什么关系？符合上述条件的点你能找出多少个？它们在哪里？(学生议一议再回答)

结论：

到线段两端距离相等的点，在这条线段的垂直平分线上。

活动三　 用直尺和圆规作线段的垂直平分线

　　 ⑴ 按课本上的方法在书上作出线段的垂直平分线；

⑵ 同桌可画出不同位置的线段，相互作出线段的垂直平分线。

(学生自己操作再合作交流。)

　　　 由“线段的垂直平分线上的点到线段两端的距离相等”和“到线段两端距离相等的点，在这条线段的垂直平分线上”，从而可以说：

线段的垂直平分线是到线段两端距离相等的点的集合。

练习：课本第19页　 练习　 1(提示，分析)、2、3(与1类似)

例1： 线段的垂直平分线外的点，到这条线段两端的距离会相等吗？为什么？

这是一道文字描述的几何说理题，对大多数同学来说容易理解，

但不容易叙述，因此要做一定的分析，引导学生展开讨论：

⑴你能读懂题目吗？题中已知哪些条件？要说明怎样一个结论？

⑵题中的已知条件和要说明的结论能画出图形来表示吗？

⑶根据图形你能说明道理吗？

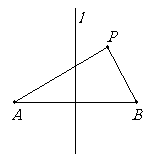
已知：直线l是线段AB的垂直平分线，点P在直线l外，

说明：线段PA、PB会相等吗？

(注意引导学生用几何语言说理)

解：线段的垂直平分线外的点，到这条线段两端的距离不会相等。(先回答问题)

说明理由如下：

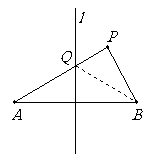
　 点P在线段的垂直平分线l外，连接PA、PB，

设PA交l于点Q，连接QB。

∵ 点Q在线段AB的垂直平分线上，

∴　 QA = QB.

(线段的垂直平分线上的点到线段两端的距离相等)

∴　 PA = PQ + QA = PQ + QB (等式性质).

∵　 PQ + QB > PB (三角形的两边之和大于第三边) ，

∴　 PA = PQ + QA> PB.

活动一　 对折线段。

问题1：按要求对折线段后，你发现折痕与线段有什么关系？(学生操作)

问题2：按要求第二次对折线段后，你发现折痕上任一点到线段两端点的距离有什么关系？(学生操作)

(这个活动学生不会有困难，易做易得出结论。教师要关注的是学生参与活动的态度是否认真，与同学交流是否积极。)

学生先思考1分钟后，再小组讨论。然后由小组中的一位同学说出讨论结果.

结论：

线段是轴对称图形，线段的垂直平分线是它的对称轴。

线段的垂直平分线上的点到线段两端的距离相等。

问题：线段是轴对称图形吗？为什么？

　 (从轴对称的定义出发，让学生说明线段是轴对称图形的理由，一方面直接提出了本课研究的主题，另一方面以为后面的操作活动提供依据。)

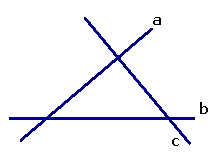如图，直线a,b,c表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，可供选择的地址有几处？如何选？