例1：已知ABC中，AB=AC=10，DE垂直平分AB，交AC于E，已知BEC的周长是16。求ABC的周长.

例2：如图，已知∠AOB及点C、D，求作一点P，使PC=PD，并且使点P到OA、OB的距离相等。

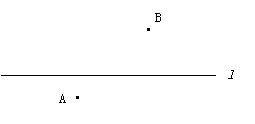例3：如图，已知直线及其两侧两点A、B。

(1)　　　 在直线上求一点P，使PA=PB；

(2)在直线上求一点Q，使平分∠AQB。

例4：如图，直线a、b、c表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，可供选择的地址有几处？如何选？

例5：已知：如图，在ΔABC中，O是∠B、∠C外角的平分线的交点，那么点O在∠A的平分线上吗？为什么？

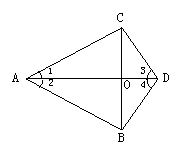
例6：如图，已知：AD和BC相交于O，∠1=∠2，∠3=∠4。试判断AD和BC的关系，并说明理由。

例7：已知：如图，△ABC中，BC边中垂线ED交BC于E，交BA延长线于D，过C作CF⊥BD于F，交DE于G，DF=BC，试说明∠FCB=∠B

例8：已知：在∠ABC中，D是∠ABC平分线上一点，E、F分别在AB、AC上，且DE=DF。

试判断∠BED与∠BFD的关系，并说明理由.

2．角的轴对称性：

①角是轴对称图形，对称轴是角平分线所在的直线。

②角平分线上的点到角的两边距离相等。

③到角的两边距离相等的点，在这个角的平分线上。

结论：角的平分线是到角的两边距离相等的点的集合

1．线段的轴对称性：

①　 线段是轴对称图形，对称轴有两条；一条是线段所在的直线，

另一条是这条线段的垂直平分线。

②线段的垂直平分线上的点到线段两端的距离相等。

③到线段两端距离相等的点，在这条线段的垂直平分线上。

结论：线段的垂直平分线是到线段两端距离相等的点的集合

P19　 1-3

3、角平分线的作法及性质；

2、垂直平分线的作法及性质；

1、线段和解老早轴对称图形；

3、P19　 3 在课本的网格线上画，可有多种不同的方法。

2、如图，用直尺和圆规作∠ADB的对称轴(即角平分线反向延长)

A

　 D　　　　　　　　　　　　　　 B

1、如图，在Rt△ABC中，DE是BC的垂直平分线，交AB于E，交BC于D，在图中找出相等的线段，说明它们相等的理由。

A

　　　　　　　　　　　　　　　　　　　　　 　E

C　　　　　　 D　　　　　　　　　　　　　　 B