
3.例题教学
例2是一道给出图形,条件明确的说理题,教学时可先让学生做出猜想,再用折纸验证,或用直尺和圆规作∠APB的平分线,观察点O与∠APB的平分线的位置,然后进行说理.
对“点P在∠AOB的平分线上吗?为什么?”这一问题的讨论,教学时要引起重视,作为学生应用所学知识解决问题的一次练习.让学生对照图形,分析已知条件,寻找解题策略,对部分有困难的学生可作适当启发.
2.探索活动
活动一 画角、折纸,探索角的轴对称性和角平分线的性质.
设计这一活动的目的是让学生经历“画图、折纸、观察、归纳”的活动过程,自主发现角的轴对称性和角平分线的性质,积累数学活动经验,提高探索能力,并让学生在活动中获得成功的喜悦.活动本身简单易做,但观察得出的结论较复杂.因此教师除组织学生认真操作外,教学时还应注意以下两点。
(1)在折纸活动中,让学生辨清角的对称轴与角的平分线的差异,理解“对称轴是角的平分线所在的直线”的含义;
(2)在得出角平分线的性质后,教师可给出这个结论的文字语言、图形语言、符合语言的不同表达形式,以帮助学生真正理解这个性质.
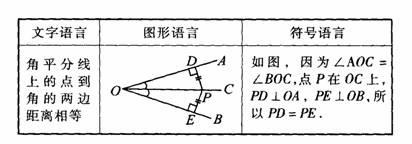
特别要注意,这个结论中,条件有两个:①即OC是∠AOB的平分线;②点P在OC上,PD⊥OA,PE⊥OB,才能得出PD=PE,两者缺一不可.如下图中PD=PE吗?各缺少了什么条件?
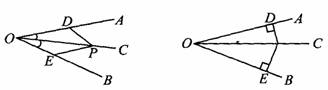
活动二 课本中的“讨论”,并作图验证所得结论.
(1)分组讨论.从轴对称的角度来剖析角平分线和线段的垂直平分线的类似特征;
(2)引导学生用类比的方法,猜想具有怎样性质的点在角的平分线上?
(3)用好课本中图1-19,验证猜想所得的结论;
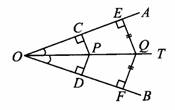
(4)在得出“到角的两边距离相等的点,在这个角的平分线上”这个结论后,教师可继续采用类比的方法,写出如下与线段的垂直平分线类似的结论:若OT是∠AOB的平分线,点P在OT上,PC⊥OA,PD⊥OB,则PC=PD;若QE⊥OA,QF⊥OB,QE=QF,则点Q在OT上.由此,可以说,角平分线是到角的两边距离相等的点的集合.
1、情境创设
(1)同学们用纸片做过纸箭和纸飞机吗?说说你的方法;
(2)试用如图所示的等腰三角形AOB纸片,折一只以点 O为箭头的纸箭,再展开纸箭,观察折痕,你有什么发现?
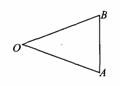
提供学生儿时喜欢玩的折纸游戏这一情境,学生有亲切感,易引起学生对折痕的关注,从而引导学生对角的轴对称性进行讨论.
4.在“操作--探究--归纳--说理”的过程中学会有条理地思考和表达,提高演绎推理能力.
[教学过程设计]
3.了解线段的垂直平分线和角平分线是具有特殊性质的点的集合.
2.探索并掌握线段的垂直平分线、角平分线的性质.
1.经历探索线段和角的轴对称性的过程,进一步体验轴对称的特征,发展空间观念.
1.4线段、角的轴对称性
(第二课时)
[教学目标]
4.小结
(1)学会了用尺规作线段的垂直平分线,知道了线段的垂直平分线是到线段两端距离相等的点的集合;
(2)经历“操作--观察--归纳--说理”的过程,发展了空间观念和演绎推理的能力.
3.例题教学
例1是一道用文字描述的几何说理题,部分学生会有困难,为此,教学时可围绕以下三个问题组织学生展开讨论:
(1)你能读懂题目吗?题中已知哪些条件?要说明怎样一个结论?
(2)题中的已知条件和要说明的结论能画出图形来表示吗?
(3)根据图形,请你说明结论成立的道理.
在讨论分析清楚后,老师可示范书写该题的解法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com