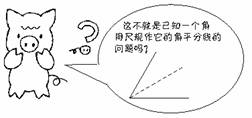
2.两条小河交汇形成的三角区，土壤肥沃，气候宜人.小猪看重了这块宝地，想在这里建一个小房子，并使房子到两条小河的距离相等，但它不知该如何选址，你能帮帮它么？

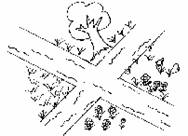
1.我们大家都喜爱放风筝.如图是一个风筝骨架.

为使风筝平衡，须使∠AOP=∠BOP.我们已知PC⊥OA，PD⊥OB，那么，PC和PD满足什么条件，才能保证OP为∠AOB角平分线呢？

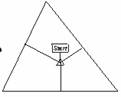
2.如右图在一三角形的小岛上，小动物们即将举行长跑比赛，比赛分三队，要求三队从岛内一点沿垂直于三边路线分别跑到小岛三边.

为公平起见，要求三起点到岛岸距离相等，你能帮它们确定起点吗？

1.我们用一张三角形的纸片，分别折出三个角的角平分线.我们发现，这三条线是交于一点的，但是，是不是所有的三角形都具有这样的性质呢？

于是，几个同学分别拿出不同形状的三角形纸片做其角平分线，观察结果.

(1)观察这几个三角形，它们的角平分线交于一点么？

(2)猜想是否任意三角形角平分线都交于一点？如果是，如何证明它呢？

1.4 角平分线

§1.4.2　 三角形三条内角平分线交于一点

如图1-38，已知∠α, 线段a. 求作：△ABC，使AB = AC,

∠A = ∠α, 角平分线AD = a.

[综合练习]

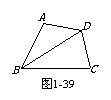已知：如图1-39，四边形ABCD中，AB < BC,　 BD平分∠ABC，且AD = CD.求证：∠A +∠C = 180°.

[探究练习]

如图1-40所示的零件由两条线段AB、CD和两条弧、组成，在工厂学工的小明同学要在工件上画出直线AB、CD交角的平分线，由于工件上没有角的顶点，小明想了很久，也没有想出怎样画这条角平分线，同学们，你们能告诉小明怎样画吗？

练习二

[基础练习] 一、1. 大于的长； 2. 30°. 二、1. B； 2. D.　 三、(略).

[综合练习]提示：在BC上截取BE = AB，连接DE.

[探究练习]提示：利用三角形三内角的平分线相交于一点.

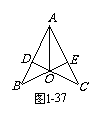
2.如图1-37，CD⊥AB, BE⊥AC, 垂足分别为D、E, BE、CD相交于点O，OD = OE, 则图中的全等三角形共有(　　　 ).

A. 1对　　　　　　　　　　 B. 2对

C. 3对　　　　　　　　　　 D. 4对

1.到三角形三边距离相等的点，是这个三角形的(　　　 ).

A.三条中线的交点　　　 　 B.三条角平分线的交点

C.三条高的交点　　　　 　 D.三边垂直平分线的交点

2.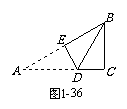一张直角三角形的纸片，如图1-36那样折叠，使两个锐角顶点A、B重合，若DE = DC, 则∠A = 　　　　°.

1.补全“作∠AOB的平分线”的作法：①在OA和OB上分别截取OD、OE，使OD = OE；②分别以D、E为圆心，以　　　　　　　　　 为半径画弧，两弧在∠AOB内交予点C；③作射线OC, OC即为∠AOB的平分线；