
3、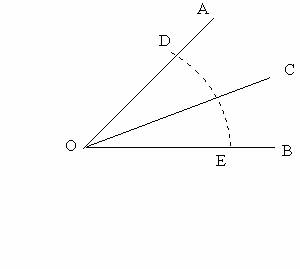 作射线OC
作射线OC
OC就是∠AOB的平分线。
读一读:尺规作图不能问题:
三等分一个任意角,倍立方--求作一个立方体,使该立方体的体积等于给定立方体的两倍。化圆为方--求作一个正方形,使其与给定圆的面积相等。
课堂练习:P32,1、2题
作业:P34,1、2、3题。
教学后记:
2、分别以D、E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内交于点C。
3、能够利用尺规作已知角的平分线。
教学过程:
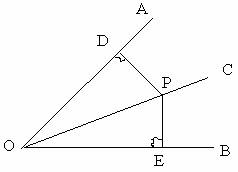
定理:角平分线上的点到这个角两边的距离相等。
证明:如图OC是∠AOB的平分线,点P在OC上
PD⊥OA,PE⊥OB,垂足分别为D、E,
∵∠1=∠2,OP=OP,
∠PDO=∠PEO=90°
∴△PDO≌△PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
其逆命题也是真命题。引导学生自己证明。
定理:在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上。
做一做:用尺规作角的平分线。
已知:∠AOB
求作:射线OC,使∠AOC=∠BOC
作法:1、在OA和OB上分别截取OD、OE,使OD=OE
2、能够证明角平分线的性质定理、判定定理及相关结论
1、进一步发展学生的推理证明意识和能力;
 如图1-34,已知:△ABC中,∠BAC
= 90°, AD⊥BC于D,AE平分∠DAC,EF⊥BC交AC于F,连接BF. 求证:BF是∠ABC的平分线.
如图1-34,已知:△ABC中,∠BAC
= 90°, AD⊥BC于D,AE平分∠DAC,EF⊥BC交AC于F,连接BF. 求证:BF是∠ABC的平分线.
[综合练习]
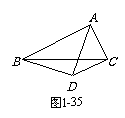 已知:如图1-35,△ABC中,AB =
2AC, AD平分∠BAC,且AD = BD. 求证:DC⊥AC.
已知:如图1-35,△ABC中,AB =
2AC, AD平分∠BAC,且AD = BD. 求证:DC⊥AC.
|
纠正错解 |
|
|
|
点 评 |
|
|
4. 角平分线
练习一
[基础练习] 一、1. AC, BD; 2. 5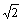 . 二、1. D; 2. A. 三、提示:证AF = EF.
. 二、1. D; 2. A. 三、提示:证AF = EF.
[综合练习]提示:作DE⊥AB, 证△ADC ≌△ADE.
2.给出下列命题:
① 垂直于同一条直线的两直线平行;
② 角平分线上的点到角两边的距离相等;
③ 三角形的三条角平分线相交于一点;
④ 全等三角形的面积相等;
其中原命题和逆命题都是真命题的共有( ).
A. 1个 B. 2个 C. 3个 D. 4个
1.如图1-33,△ABC中,∠B = 42°, AD⊥BC于D,E是BD上一点,EF⊥AB于F,若ED = EF, 则∠AEC的度数为( );
 A. 60° B. 62° C. 64° D. 66°
A. 60° B. 62° C. 64° D. 66°
2.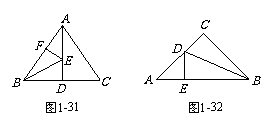 已知:如图1-32,在Rt△ABC中,∠C =
90°, AC = BC, BD平分∠ABC交AC于D, DE⊥AB于E,若BC =
5, 则△DEC的周长为 .
已知:如图1-32,在Rt△ABC中,∠C =
90°, AC = BC, BD平分∠ABC交AC于D, DE⊥AB于E,若BC =
5, 则△DEC的周长为 .
1.如图1-31,△ABC中,AD是BC的垂直平分线,BE平分∠ABC交AD于E, EF⊥AB , 则AB = ,BF = ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com