2.能够证明三角形的三条角平分线相交于一点的定理；

1.进一步加强学生推理证明的能力；

本节课的内容是在上一节课的基础上证明了三角形三条角平分线相交于一点的问题，证明思路和方法依照三角形三边的垂直平分线相交于一点进行思考，并为以后学习三角形的内切圆打下基础，安排的例题是使学生进一步理解掌握运用所学定理的综合运用.

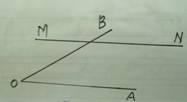
2．如图(3)，在直线MN上找一点P，

使点P到射线OA、OB的距离相等.

　　　　　　　　　　　　　　　　　　　　　　　　　 图 3

1.已知：如图(2)，∠C=∠C′=90°，AC=A C′.　

求证：①∠ABC=∠AB C′

②BC=B C′(要求不用三角形全等的判定) 　　　　　图2

1.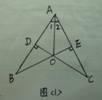已知：如图(1)，CD⊥AB，BE⊥AC，垂足分别为D、E，BE和CD相交于点O.

求证：①当∠1=∠2时，OB=OC；

②当OB=OC时，∠1=∠2 .

3.画一个等腰直角三角形，在它的斜边上求一点，使它到两条直角边的距离相等(不写画法).量一下这点到直角边的距离与直角边长有什么关系？这一点与三个顶点的距离有什么关系？

练习二

2.角平分线上的点到这个角的两边的距离___________________.

练习一

1.到一个角的两边距离相等的点，一定在___________________.