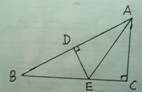
1.已知：如图(3)，△ABC中，AB=AC，∠A=90°，

BD是角平分线，过点D作DE⊥BC，垂足为点E，

求证：AD=DE=EC .

2.已知：如图(1),△ABC中，AB=AC，∠1=∠2.

求证：AD平分∠BAC.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图1

练习二

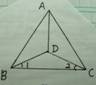
已知：如图(2)，等边三角形ABC的三条中线相交于O，

在图中找出所有等腰三角形，并证明你的结论.

练习一

1.和三角形三边距离相等的点一定在__________________.

在推理证明的过程中，转化思想是行之有效的手段，所谓转化思想就是条件与条件之间的勾通与连接.即“桥梁”的作用，使要证明的结论顺利解决.用好转化思想是学好几何推理证明的重要数学方法.

根据所学三角形的三条内角平分线相交于一点的定理和已学过的定理，解决有关的几何证明问题.

在证明过程中，教师应注意提醒学生运用简单的方法证明，防止学生绕远路、再证三角形全等.

圆规、直尺、直角三角板.

重点：三角形三条角平分线相交于一点的证明.

难点：多个定理的综合应用.

3.初步掌握综合运用多个定理解决有关问题的思路和方法.