2. 当a、b是怎样的数值时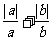，有最大值，求出这个值有最小值吗？何时为0？

　　 分析：a、b是不为0的有理数，可能都是正数、负数，也有可能是一个正一个负，本题渗秀分类讨论的思想。

　　 解：1. (1)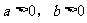

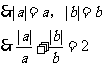
　　 (2)

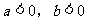
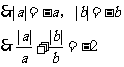
　　 (3)a、b异号

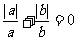
1. 的值可能是多少？说出理由。

3. 数形结合的思想：利用数形结合，可以使所要研究的问题化难为易，化繁为简。

　　 用数轴上的点来表示有理数，就是最简单的数形结合思想的体现。结合数轴表示有理数，对于理解有理数的绝对值、相反数等概念以及有理数大小的比较等，更有直观性。

　　 数形结合法，它是今后学习中的一种重要方法。在其它科目的学习中，也要结合直观的图形去解决抽象的问题，结合日常生活中的现象去学习书本中的知识，这样能帮助我们分析问题、解决问题，使较难的问题简单化。

[典型例题]

　　 例1. 如果数轴上有两点A、B，表示的数分别为a、b，在数轴上标出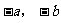，并用“<”号连接。

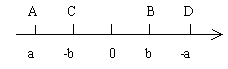
　　 分析：涉及了数轴的相关知识，利用比较大小知识点来解

　　 解：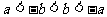

　　 例2. 计算

　 　分析：两个相邻数之差为，共有25个这样的。

　　 解：原式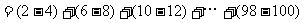

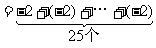
　　 例3. 计算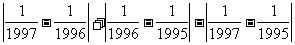

　 　分析：利用绝对值的知识解决

　　 解：原式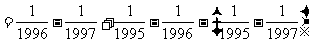

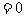
　　 例4. a、b、c是小于4的连续整数，且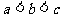，若，求a、b、c的值。

　　 解：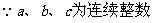

　　 (2)

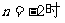
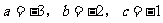
　　 (3)n=0时，

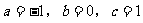
　　 例5. 若a、b是都不为0的有理数

2. 分类讨论的思想：当被研究的问题包含多种可能情况，不能一概而论时，必须按可能出现的所有情况来分别讨论，得出各种情况下相应的结论。这种处理问题的思维方法称为分类思想。

　　 本章在研究相反数、绝对值、有理数加法法则、乘法法则、乘方运算的符号法则等，都是按有理数分成正数、负数、0三类分别研究的。

　　 分类必须遵循以下两条规则：

　　 (1)每一次分类要按照同一标准进行；

　　 (2)不重复、不遗漏。

　　 例如：如果把有理数分为正数和负数两类，漏掉了零，就错了。

1. 探究观察法：在有理数这一章中的一些主要概念和性质，例如，数轴、相反数、绝对值、有理数大小比较、有理数的运算法则和运算律的研究都离不开观察。

(三)有理数运算

　 1. 运算法则：

　　 (1)加法法则：

　　 同号两数相加取相同的符号，并把绝对值相加；异号两数相加，绝对值相等时和为0，绝对值不等时，取绝对值较大的数的符号，并用较大绝对值减去较小绝对值，一个数同0相加仍得这个数。

　　 (2)减法法则：

　　 减去一个数等于加上这个数的相反数

　　 (3)乘法法则：

　　 两数相乘，同号为正，异号为负，并把绝对值相乘，n个不等于0的数相乘积的符号由负因数的个数决定，当负因数有奇数个时，积为负，当有偶数个时，积为正。n个因数中有一个为0则积为0。

　　 (4)除法法则：

　　 ①除以一个数等于乘以这个数的倒数。

　　 ②两数相除，同号得正，异号得负，并把绝对值相除。

　　 ③0除以任一个不等于0的数都得0。

　　 (5)乘方的意义：

　　 求n个相同的因数的积的运算。

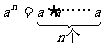
　　 (6)乘方法则：

　　 正数的任何次幂都是正数，负数的奇次幂是负数，负数的偶次幂是正数，零的任何次幂都是零。

　 2. 运算律：

　　 (1)加法交换律：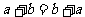

　　 (2)结合律：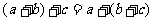

　　 (3)乘法交换律：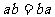

　　 (4)乘法结合律：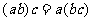

　　 (5)分配律：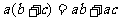

　 3. 运算顺序：

　　 先算乘方，再算乘除，最后算加减，如果有括号就先算括号里的，同级运算从左向右进行运算。

(二)有理数比较大小：

　 1. 正数都大于零，负数都小于零，即负数<零<正数

　 2. 两个正数绝对值大的数较大，两个负数绝对值大的数反而小

　 3. 在数轴上右边的数总比左边的数大

(一)有理数的有关概念

　 1. 有理数是整数和分数的总称。

　 2. 有理数的分类：

　 3. 数轴：规定了原点、正方向和单位长度的直线

　 4. 相反数：绝对值相等、符号相反的两个数互为相反数。零的相反数是零。从数轴上看，表示互为相反数的两个点分别在原点两侧，并与原点的距离相等。

　 5. 绝对值：一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，零的绝对值是零。绝对值等于它本身的数是非负数。

　　 从数轴上看一个数的绝对值就是表示这个数的点与原点的距离。

　　 (1)

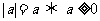
　　 (2)

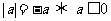
　　 注意不要丢掉“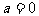”的情况。

　 6. 倒数：乘积为1的两个数互为倒数。

　　 零没有倒数，通常用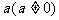与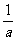表示一对互为倒数的数。倒数等于它本身的数是。

1.4、角平分线(一)

2.已知：如图(4)，在△ABC中，∠C=90°，

D是斜边AB的中点,AB=2AC,过D作DE⊥AB，

交BC于点E，求证：①AE平分∠BAC;

②AE=BE .　　　　　　　　　　　　　　　　 图4