2、思考、讨论：

等边三角形有什么性质：

(1)是轴对称图形，有三条对称轴；

(2)每个内角都等于60°，也称正三角形；

(3)具有等腰三角形所具有的所有性质；

1、讨论、交流

等腰三角形是轴对称图形吗？说说你的理由.(重合)

∠B与∠C相等吗？怎么说明？(全等)　　　　　　　　　　 腰　　　　　 腰

图(3)中的痕迹有什么性质(合作、讨论)

(1)等腰三角形是轴对称图形，有一条对称轴；　　　　　　　　　 底角　　　 底角

(2)等腰三角形两个底角相等.(等边对等角)　　　　　　 B　　　 底边　　　　 C

(3)等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合(三线合一)

1、操作、实践：

取一等腰三角形纸片，照图折叠，你能得到什么结论？

A　　　　　　　　　 A　　　　　　　　　　　　 A

　　　　 B　　　　　 C　　　　　　　　　　 B(C) 　　B　　　　　　 C

(1)　　　　　　　　 (2)　　　　　　　　　　 (3)

3、如图，已知：△ABC是等边三角形，且AD＝BE＝CF，那么△DEF是等边三角形吗？

2、如图，△ABE和△ACE都是等边三角形，BD与CE相交于点O。

(1)EC＝BD吗？为什么？若BD与CE交于点O，你能求出∠BOC的度数是多少吗？

(2)如果要△ABE和△ACD全等，则还需要什么条件？在此条件下，整个图形是轴对称图形吗？此时∠BOC的度数是多少？

1、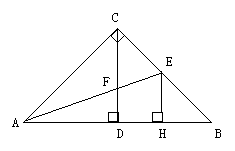如图，在△ABC中，∠ACB＝90°，高CD和角平分线AE交于点F，EH⊥AB于点H，那么CF＝EH吗？说明理由。

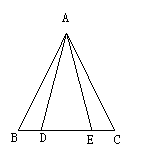
例1、如图，已知D、E两点在线段BC上，AB＝AC，AD＝AE，试说明BD=CE的理由?

例2：如图，已知：△ABC中，AB＝AC，BD和CE分别是∠ABC和∠ACB的角平分线，且相交于O点。①试说明△OBC是等腰三角形；②连接OA，试判断直线OA与线段BC的关系？并说明理由。

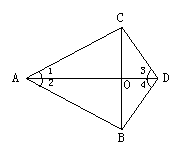例3：如图，已知：AD和BC相交于O，∠1=∠2，∠3=∠4。试判断AD和BC的关系，并说明理由。

例4：如图，已知：△ABC中，∠C=90⁰，D、E是AB边上的两点，且AD=AC，BD=BC。

求∠DCE的度数。

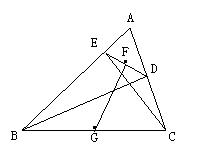例5：如图，已知：△ABC中，BD、CE分别是AC、AB边上的高，G、F分别是BC、DE的中点。试探索FG与DE的关系。

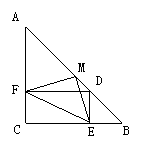例6：如图，已知：△ABC中，∠C=90⁰，AC=BC，M是AB的中点，DE⊥BC于E，DF⊥AC于F。试判断△MEF的形状？并说明理由。

例7：如图，已知：△ABC为等边三角形，延长BC到D，延长BA到E，AE=BD，连结EC、ED，试说明CE=DE。

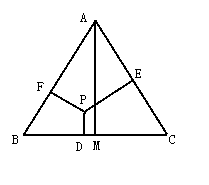
例8：如图，在等边△ABC中，P为△ABC内任意一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，AM⊥BC于M，试猜想AM、PD、PE、PF之间的关系，并证明你的猜想．

4．三角形的分类：

　　　　　　　　 斜三角形：三边都不相等的三角形。　　　　　

　　　　 三角形　　　　　　　　 只有两边相等的三角形。

　　　　　　　　 等腰三角形

　　　　 　　　　　　　　　　等边三角形

3．等边三角形：

① 等边三角形的定义：

三边相等的三角形叫做等边三角形或正三角形。

②　 等边三角形的性质：

等边三角形是轴对称图形，并且有3条对称轴；

等边三角形的每个角都等于60⁰。

③等边三角形的判定：

3个角相等的三角形是等边三角形；

有两个角等于60⁰的三角形是等边三角形；

有一个角等于60⁰的等腰三角形是等边三角形。

2．　　　　　　　　 等腰三角形的判定：

①如果一个三角形有2个角相等，那么这2个角所对的边也相等；(简称“等角对等边”)

②直角三角形斜边上的中线等于斜边上的一半。