
这节课你学到了什么?学生自己总结:
⑴ 等边三角形是底和腰相等的等腰三角形,有3条对称轴,每个角都是60o.
⑵ 有3个角相等的三角形是等边三角形;
有2个角等于60o的三角形是等边三角形;
有1个角等于60o的等腰三角形是等边三角形.
⑶ 在解决等腰三角形的边、角问题时,应当恰当地运用分类讨论的思想方法.
课本第28页 练习 1、2(提示,分析)
⑴重视解题前的“分析”. 通过分析,使学生知道在等腰三角形中,已知一个角的度数求解问题时,通常应分类讨论,因为这个角可以是顶角,也可以是底角. 同样,已知等腰三角形的一边时,通常应考虑这边是腰和底两种情况.
例3
 有一个角等于的等腰三角形是等边三角形吗?为什么?
有一个角等于的等腰三角形是等边三角形吗?为什么?
解: 设等腰三角形△ABC中,AB=AC.
⑴如果顶角∠A=60o,如图⑴.
∵ AB=AC, ∴ ∠B=∠C(等边对等角).
又 ∠A+∠B+∠C=180o,
∴ ∠B=∠C=60o,即 ∠A=∠B=∠C=60o.
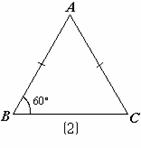 ∴ AB=BC=AC(等角对等边).
∴ AB=BC=AC(等角对等边).
⑵如果底角∠B=60o,如图⑵.
∵ AB=AC, ∴ ∠C=∠B=60o(等边对等角).
又 ∠A+∠B+∠C=180o,
∴ ∠A=60o,即 ∠A=∠B=∠C=60o.
∴ AB=BC=AC(等角对等边).
综上所述,有一个角等于的等腰三角形是等边三角形.
⑵为让学生进一步熟悉等边三角形和等腰三角形的性质,激发学生学习的兴趣,可根据教学实际选用如下的例题。
用1-3种不同的分割方法,将1个等边三角形分割成4个等腰三角形.
活动一 课前准备一个等边三角形的小纸片:
⑴用折纸的方法找出它的对称轴,你有什么发现?
⑵用量角器量出3个角的大小:
⑶通过折纸和度量,你得出了等边三角形的哪些特殊性质?
三边相等的三角形叫做等边三角形或正三角形.
因为等边三角形是特殊的等腰三角形,所以它除了具有等腰三角形的一切性质外,还具有更特殊的性质.
等边三角形是轴对称图形,并且有3条对称轴。(哪3条?为什么?)
等边三角形的每个角都等于60o。(为什么?)
应用格式:
 在△ABC中,
∵AB=BC=AC, ∴∠A=∠B=∠C=60o.
在△ABC中,
∵AB=BC=AC, ∴∠A=∠B=∠C=60o.
活动二 课本中的“思考”.
⑴两人一组开展拼图、画图活动,并回答:用两块
相同的含有60o的直角三角尺拼成右图.
①∠A、∠B、∠ACB相等吗?
②量出AB、BC、CA的长度,你发现了什么?
沿直线l平移其中的一块三角尺使点B到点D,
延长斜边交AC的延长线于点E,量出AD、DE、
AE的长度,你发现了什么?
⑵教师在活动中要关注学生说理是否正确,
层次是否清楚,努力提高学生的数学素养,积累活动经验.
2、问题:有一个等腰三角形,它的底边和腰恰好相等,这样的三角形具有什么性质?
(引导学生从等边三角形是特殊的等腰三角形这一角度来认识等边三角形,有助于理解它们的从属关系,也便于由等腰三角形的性质推出等边三角形的性质。)
1、复习等腰三角形的有关性质:
|
文字语言 |
图形语言 |
符号语言 |
|
等边对等角 |
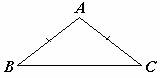 |
在△ABC中,∵AB=AC, ∴∠B=∠C(等边对等角). |
|
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合 |
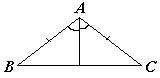 |
在△ABC中, ∵AB=AC,∠BAD=∠CAD ∴BD=CD,AD⊥BC(三线合一). |
|
等角对等边 |
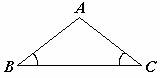 |
在△ABC中,∵∠B=∠C, ∴AB=AC (等角对等边). |
|
直角三角形斜边上的中线等于斜边的一半 |
 |
在△ABC中,∵∠ACB=90o,AD=BD, ∴CD=AD=BD= 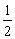 AB(……). AB(……). |
课本第29页 习题1.5 6、7、8、9
2、直角三角形斜边上的中线等于斜边的一半。
1、等角对等边的性质;
课本第26页练习1、2、3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com