
例2 如图,在等腰梯形ABCD中,AB∥DC,AD=BC,点E、F分别在两腰AD、BC上,且EF∥DC. 梯形CDEF是等腰梯形吗?为什么?
分析:①从已知等腰梯形ABCD你能得到什么(性质)?
②四边形CDEF为什么是梯形?
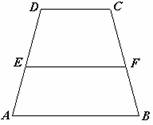 ③怎样说明梯形CDEF也是等腰梯形(判定)?
③怎样说明梯形CDEF也是等腰梯形(判定)?
解 四边形CDEF是等腰梯形.
在等腰梯形ABCD中,
∵ AB∥DC,AD=BC,
∴ ∠D=∠C(等腰梯形在同一底上的两个角相等).
∵ EF∥DC,即四边形CDEF是梯形,
∠D=∠C(由上)
|
(在同一底上的两个角相等的梯形是等腰梯形)
2、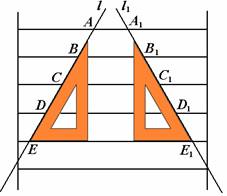 操作、验证:
操作、验证:
读句画图,验证猜想.
如图,用三角尺在横格纸上画直线和直线,
能用图中字母表示的梯形(如梯形ABB1A1、
梯形BD D1B1)是等腰梯形吗?为什么?
∵ BD∥B1D1,即四边形BD D1B1是梯形,
∠BDD1=∠B1D1D=60o,
∴ BD=B1D1,即梯形BD D1B1是等腰梯形.
(在同一底上的两个角相等的梯形是等腰梯形)
1、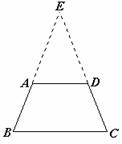 探索思考:
探索思考:
当梯形同一底上的两个角相等时,这个梯形会不会是等腰梯形呢?
如图,梯形ABCD中,AD∥BC,如果∠B=∠C,问“AB=DC”
成立吗?
分别延长BA、CD相交于点E,
在△EBC中,∵ ∠B=∠C, ∴ EB=EC(等角对等边).
∵ AD∥BC,
∴ ∠EAD=∠B,∠EDA=∠C(两直线平行,同位角相等).
∴ ∠EAD=∠EDA.
在△EAD中,∵ ∠EAD=∠EDA,∴ EA=ED(等边对等角).
∴ EB-EA=EC-ED. 即AB=DC.
从而,有等腰梯形的判定方法:
在同一底上的两个角相等的梯形是等腰梯形.
注意:应用此判定方法的条件有二,①“梯形”,②“同一底上的两个角相等”.
等腰梯形与等腰三角形有着紧密的联系.比照等腰三角形的特性,你对等腰梯形还有什么想法?试把你的想法写在下表的空格内:
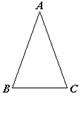 在△ABC中 |
如果AB=AC, 那么∠B=∠C. |
如果∠B=∠C, 那么AB=AC. |
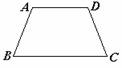
在梯形ABCD中, AD∥BC |
⑴如果AB=AC, 那么∠B=∠C; ⑵如果AB=AC, 那么∠A=∠D. |
? |
怎样说明你的猜想是正确的呢?
(类比是发现新知、寻找规律、解决问题的一种重要方法.课本假设了等腰梯形与等腰三角形进行类比的情境,引导学生自然而然地提出“当梯形同一底上的两个角相等时,这个梯形会不会是等腰梯形呢”的猜想,同时萌生去探索这一想法是否正确的欲望)
课本第34页习题1.6 1、2、3、4
2、经历了探索活动,提高了说理的能力.
1、等腰梯形性质:
⑴等腰梯形是轴对称图形,有一条对称轴,这条对称轴是过两底中点的直线;
⑵等腰梯形在同一底上的两个角相等;
⑶等腰梯形的对角线相等.
课本第32页练习 1、2、3
3、讨论、交流(例题教学):
例1 如图,在梯形ABCD中,AD∥BC,AB=DC,AC、BD相等吗?为什么?
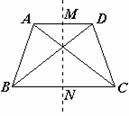 分析:可从等腰梯形的轴对称性说明,也可从“等腰梯形在同一底上的两个角相等”及全等的知识等多方面来说明。
分析:可从等腰梯形的轴对称性说明,也可从“等腰梯形在同一底上的两个角相等”及全等的知识等多方面来说明。
解法1 AC=BD.
如图,过两底中点M、N作直线l.
∵ M、N分别是底AD、BC的中点,
∴ 直线l是等腰梯形ABCD的对称轴.
(过等腰梯形两底中点的直线是它的对称轴)
∵ 点A与点D是对称点,B点与点C是对称点,即是对称线段,
∴ AC=BD.
(注意体会用轴对称法解题之妙处)
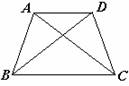 解法2 AC=BD.
解法2 AC=BD.
如图,在梯形ABCD中,
∵ AD∥BC,AB=DC,
∴ ∠ABC=∠DCB(等腰梯形同一底上的两个角相等).
在△ABC和△DCB中,
∵ AB=DC,∠ABC=∠DCB,BC=CB,
|
∴ AC=BD(全等三角形对应边相等).
从而,得出等腰梯形的又一个性质:
等腰梯形的对角线相等.
应用格式:
在梯形ABCD中,
∵ AB∥CD,AD=BC,
∴ AC=BD(等腰梯形的对角线相等).
2、探索思考:
等腰梯形是轴对称图形吗?它具有哪些性质?
等腰梯形是轴对称图形,过两底中点的直线是它的对称轴.
等腰梯形在同一底上的两个角相等.
如图,在梯形ABCD中,AB∥CD,AD=BC,
E、F分别是AB、CD的中点,那么,EF所在直线是它的对称轴.
 (注意:对称轴是直线)
(注意:对称轴是直线)
在梯形ABCD中,
∵ AB∥CD,AD=BC,
∴ ∠A=∠B,∠C=∠D(等腰梯形在同一底上的两个角相等).
(根据下文解题需要,结论不一定要写全)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com