1．情境创设

　　 (1)出示“梯子”、“水渠横断面”、“跳箱”等一些含有等腰梯形的图案、照片、实物模型，让学生找出这些图案、照片、实物模型中的等腰梯形，指出等腰梯形的腰和底；

　　 (2)举出生活中见到的含有等腰梯形的实物，并与同学交流；

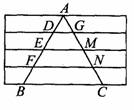
(3)如图，在横格纸上画一个等腰三角形ABC，找出图中的等腰梯形．

4．在等腰梯形的性质和判定条件的探究过程中，进一步学习有条理地思考和表达，体会转化、类比等数学思想方法在解决问题中的作用．

　 [教学过程设计]

1．6等腰梯形的轴对称性

(第一课时)

[教学目标]

1．操作题：请同学们拿出事先准备好的等腰直角三角形和等腰三角形，从中剪出等腰梯形来，并与同学交流

由学生讨论后得出结论：作直角三角形的斜边和等腰三角形底边的平行线就可得到等腰梯形

　
　
　
　
　
　 学生可以举出一些梯形的实例来。
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
学生操作
小组讨论
　
　
　
　
　
让学生感受生活中处处有数学
　
　
　
　
　
　
　
　
　
　
　
　
让学生动手剪不但可以理解等腰梯形的概念更可以培养学生的数学兴趣
2、操作题(1)将等腰梯形剪下来取上下底的中点并连接。　　　　　 A　　　　 B
　　　　　　　
　
C　　　　　　　 D
(2)将图形沿连线折叠
小组讨论下面的问题：①折叠后图形怎么样。
　　　　　　　　　　 ②你发现等腰梯形是一个什么图形。
讨论后得出结论：等腰梯形是一个轴对称图形。
　　　　　　　　　　 ③对称轴是什么？
在这个问题上学生很容易出现下面的问题比如说：等腰梯形的对称轴是上下底中点之间的线段。
正确的应该是等腰梯形的对称轴是过上下底的中点的直线
　　　　　　　　　　　 ④∠A和∠B　 ,∠c 和∠D是什么关系？
　 学生很可能会得出下面的结论；等腰梯形的两底角相等。
　在这个地方，师一定要强调等腰梯形的同一底边上的两底角相等
上面的几个结论用几何语言表示那就是在梯形ABCD中
AB∥CD,AC＝BD,EF分别是AB,CD的中点，那么EF所在的直线是它的对称轴，∠A＝∠B,∠C＝∠D.(结合上图)
三、随堂演练　 课本第32页第2、3题
补充、①如图、在梯形ABCD中，如果AD∥BC,AB＝CD,∠B＝60°,AC⊥AB,那么∠ACD＝____,∠D＝____.
A　　　　　　　 D　　　　　　　　　　　 D
　　　　　　　　　　　　　　 A　　
　　　　　　　　　　 C
B　　　　　　　　　　　　　 B　　　　　　　　 C
　　　　　　　　　　　　 E
②在梯形ABCD中，BC∥AD,DE∥AB,DE＝DC,∠A＝100°则∠B＝____,∠C＝____,∠ADC＝____,∠EDC＝____.　　　　　　　　　
　
　
四．学生操作　
连接刚才剪下来的等腰梯形的对角线
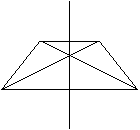议一议：⑴对角线的交点在什么位置？
　　　 ⑵两条对角线有什么特殊关系？为什么？
　　　　　　 A　 M　 B
　　　　　　　
　　　　　　　　 O
C　　　　　　 N　　　　　 D
　　 　　　　　　　L　　　　　　　
　
这道题说理要求很严密，所以在讲授时要学生特别注意说理过程。
师分析：过两点中点M,N作直线L.
根据(因为)“过等腰梯形两底中点的直线是等腰梯形的对称轴”，
点A与点B是对称点，点C与点D是对称点，即AD与BC是对称线段。
所以AD＝BC
强调格式(因为-------所以-------)
　 或者(根据--------所以-------)
　　 ⑶你能从中得到什么结论？
　　　　　　　 (小组讨论)
　 师生一起总结：等腰梯形的对角线相等
五．随堂演练
1.如图所示，在梯形ABCD中，已知AB∥CD,AD＝BC,AC 和BD相交于点O,试说明OD＝OC
D　　　　 C
AB　
　 2．如图，梯形ABCD中，AD∥BC,AB＝DC,　 ∠ACB＝40°,∠ACD＝30°.
　　 ⑴∠B＝___°,∠D＝___°,∠BAC＝___°
　　 ⑵如果BC＝5cm,连接BD,求AC,BD的长，并说明理由。
　　　　　　　 A　　　　 　　D
　
　
　　　　　　 B　　　　　　　　 C
六．小结回顾
本堂课我们学习了等腰梯形的性质，分别是那些内容？在进行说理的时候应该注意什么
七．课后巩固
课本P46 T12,13　　　　
　
　
学生总结结论
　
　
　
　
　
　
　
学生操作
　
　
　
　
　
　
　
小组讨论，师生合作　
　
　
　
　
　
　
　
学生要特别注意是直线
　
　
　
　
　
　
注意一定要是同一底边
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
同桌交流
　
　
　
学生要特别注意说理的过程
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
学生讨论
　
　
学生练习并交流结果
　
　
　
　
　
　
　
学生回忆并回答
　
设计的目的主要是让学生自己发现问题，解决问题，从而提高学习的自主性
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
安排这个练习主要是为了训练学生对梯形性质的理解和应用。
　
　
　
　
　
　
　
　
　
　
让学生自己发现问题，加深对问题的理解
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
安排的目的是：
学生通过练习能掌握等腰梯形对角线相等这一个性质，并且能加强说理能力

学生谈本节课的收获：

　 什么样的梯形是等腰梯形　

2、例题的讲授：

　　 例2、如图，等腰梯形ABCD中，点E、F分别在两腰AD、BC上，且EF∥DC，梯形CDEF是等腰梯形？为什么？