某同学用一张正方形纸片折小船，但他手头上没有现成的正方形纸片，于是他撕下一张作业本上的纸，按照如图，沿AE对折使点B落在点F的位置上,再把多余部分FECD剪下,如果他事先量得矩形ABCD的面积为90cm²,又测量剪下的多余的矩形纸片的面积为40cm².请根据上述条件算出剪出的正方形纸片的边长是多少厘米.

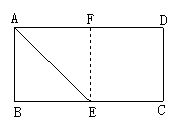
　　 将原矩形纸片的面积减去剩余的矩形纸片的面积即为正方形纸片的面积,正方形纸片的面积为90-40=50cm²,而正方形的面积为边长的平方,要求正方形的边长就得算出多少的平方等于50,但我们知道7²=49,8²=64,50这个数既不是7²,也不是8²,由于49<50<64,故此正方形的边长应大于7而小于8.到底它为多少呢?它是一个小数吗?你有什么办法确定这个值呢?这一系列问题正是我们这节课要讨论的问题.

2.了解无理数的发现过程，鼓励学生大胆质疑，培养学生学习数学的热情。

　　 教材解读

　　 本节内容首先给出一个简单的问题，根据正方形的面积求出其边长，由此引出求某数的平方根的问题，在涉及到不能直接用已有的知识开方时，则引进计算器的使用方法，通过计算器对任意正数进行开方。这样将有理数与无理数沟通起来成为实数。

　　 学情分析

　　 上学期已经学习了有理数，对任何数的形式主义都能够顺利得到，同时也感知了“互为相反数的平方相等”，故由平方值去探索平方根的问题实际上只是互逆过程，只要求出一个数的平方就可得知平方根的值。

1.引导学生充分进行交流，讨论与探索等教学活动，培养他们的合作与钻研精神。

　　 采用类比平方值的求法，定义出平方根的概念，同时从这个过程可知一个什么样的数才具有平方根，这种数有几个平方根？并比较这两个平方根之间有什么关系？

2.对于任意有理数都能区分其“+”、“－”性，运用计算器已势在必行。

1.通过对平方值的计算等确立平方根的意义、开方的运算。了解算术平方根与平方根的区别与联系。毛

(三)探究拓展

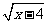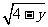　　 6.若与互为相反数,求xy的算术平方根.

(二)创新提升

　　 5.已知2a-1的算术平方根是3,3a+b-1的算术平方根是4,求a、b的值.

(一)双基练习

　　 1.某数的算术平方根等于它本身,则这个数为_______;若某数的算术平方根为其相反数,则这个数为______.

2.求下列各式的值:

,, 　, ,

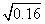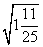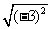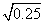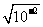
　　 3.3x-4为25的算术平方根,求x的值.

　　 4.已知9的算术平方根为a,b的绝对值为4,求a-b的值.

(三)归纳总结,知识回顾

　　 这节课主要就平方根中的算术平方根进行讨论,求一个数的算术平方根与求一个正数的平方幂正好是互逆的过程,因此,求正数的算术平方根实际上可以转化为求一个数的开平方运算.只不过,只有正数和0才有算术平方根,负数没有算术平方根.

　　 练习设计