
1.


 方程组① x-y=4 ② 2x-y=5 ③ y=3x
④ x-5=3y
方程组① x-y=4 ② 2x-y=5 ③ y=3x
④ x-5=3y
xy=3
y=4x+1
x+4z=8
 -
- =
=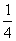
 ⑤ x-5=3y
⑤ x-5=3y
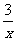 +y=1中二元一次方程组的个数是
( )
+y=1中二元一次方程组的个数是
( )
A、1 B、2 C、3 D、4
[例1]判断下列方程组,是否为二元一次方程组,并说明理由.




 (1)x-y= 3 (2)
(1)x-y= 3 (2) 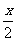 -y=5 (3) x-2y+xy=5 (4)
-y=5 (3) x-2y+xy=5 (4) 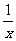 -y=3 (5) x=5
-y=3 (5) x=5
y+z=4
x+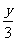 =1
x=y
x+3y=1
3y-4x=1
=1
x=y
x+3y=1
3y-4x=1
解:(1)不是二元一次方程组,因为方程组中所会的未知数不是两个,而是三个.
(2)是二元一次方程组,符合二元一次方程组的定义.
(3)不是二元一次方程组,因为方程x-2y+xy=5不是一次方程,而是二次方程.
(4)不是二元一次方程组,因为方程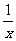 -y=3不是整式方程,一定不是一次方程.
-y=3不是整式方程,一定不是一次方程.
(5)是二元一次方程组,符合二元一次方程组的定义.
(以上分析可让学生尝试回答后,老师点评)
师点评:二元一次方程组的定义要落实到关键的两个词上“二元”,“一次”,判别时,可先看方程组中未知数的个数是否为两个,再看方程组中的两个方程是否都为一次方程,只有同时满足“二元”与“一次”这两个条件的方程组,才为二元一次方程组.
2]若关于x,y 的方程3x3m+2n-5y-2m-3n=7是二元一次方程,根据题意可列出关于m、n的方程组为
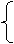 解:根据题意,得 3m+2n=1
解:根据题意,得 3m+2n=1
--2m-3n=1
师点评:所谓关于x,y 的方程,即指在此方程x,y为未知数,而其他字母如m,n 都当已知数看待.
[例3]为奖励在读书知识竞赛中的获奖同学,赵欣代表班委会去购买两种笔记本作为奖品,已知甲种笔记本为5元/本,乙种笔记本为3元/本,共购买了10本,花去了34元,如果设甲种笔记本购买了x本,乙种笔记本购买了y本,请根据题意,列出两种笔记本各买了几本的方程组.
思路分析:
本题中两种笔记本的单价,购买的总数,所花的总费用是已知的,可找出“购买甲种笔记本的数量+购买乙种笔记本的数量=10(本)”“购买甲种笔记本的费用+购买乙种笔记本的费用=34(元)”,由这两个等量关系式,即可列出方程组.
解:设甲种笔记本购买了x 本,乙种笔记本购买了y本.
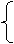 由题意得 x+y=10
由题意得 x+y=10
5x+3y=34
[问:若设购买甲种笔记本共花去m元,购买乙种笔记本共花去n元,则该怎样列方程组?]
点评:列方程组解应用题,审题是前提,找出等量关系是关键,审题必须弄清各个量表示的含义,单位及量之间的数量关系,找出等量关系,再把已知量、未知量代入关系式,“翻译”成方程(组).
问题一:今有鸡、兔同笼,上有35头,下有94足,问鸡兔各几何?
 分析:“上有35头”,指鸡、兔共35只,即“鸡的只数+兔的只数=35(只),”“下有94足”,指鸡的腿与兔的腿共有94条,即“鸡腿的条数+兔腿的条数=94(条)”若设鸡有x只,兔有y只,则 x+y=35
分析:“上有35头”,指鸡、兔共35只,即“鸡的只数+兔的只数=35(只),”“下有94足”,指鸡的腿与兔的腿共有94条,即“鸡腿的条数+兔腿的条数=94(条)”若设鸡有x只,兔有y只,则 x+y=35
2x+4y=94
问题二:某班学生39人,到公园划船,共租用9艘船,每艘大船可坐5人,每艘小船可坐3人,每艘船都坐满.问:大船、小船各租了多少艘?
 分析:设大船租了x艘,小船租了y艘,根据题意得 x+y=9
分析:设大船租了x艘,小船租了y艘,根据题意得 x+y=9
5x+3y=39
像上述①、②这样,含有两个未知数的两个一次方程所组成的方程组叫做二元一次方程组.
 师:二元一次方程组,教材上只给出了描述性意义,重在看其形式,究其本质是方程组中两个方程都是一次方程(即“一次”),同时方程组中只有两个(两种)未知数(即“二元”)要从这个层面上理解二元一次方程组的定义,如 x=a
师:二元一次方程组,教材上只给出了描述性意义,重在看其形式,究其本质是方程组中两个方程都是一次方程(即“一次”),同时方程组中只有两个(两种)未知数(即“二元”)要从这个层面上理解二元一次方程组的定义,如 x=a
y=b (a、b为常数)就是二元一次方程组.
课本第124页A组 l.
课本第124页A组 l.
3.选择题
(1)下列近似数中,精确到千位的是( )
A.1.3万 B.21.010
C.1018 D.15.28
(2)有效数字的个数是( )
A.从右边第一个不是0的数字算起
B.从左边第一个不是0的数字算起
C.从小数点后的第一个数字算起
D.从小数点前的第一个数字算起
2.填空题
(1)3.14精确到________位,有_________有效数字
(2)0.0102精确到_________位,有效数字是__________
(3)精确到__________位,有效数字是___________
1.判断下列各题中的效,哪些是准确数,哪些是近似数?
(1)小明到书店买了10本书
(2)中国人口约有13亿
(3)一次数学测验中,有5人得了100分
(4)小华体重约54千克
(四)归纳小结
师生共同小结(1)有效数字的意义及两个注意点;(2)带单位的近似数(为2.3万)和用科学记数法表示的近似数的精确度和有效数字的求法.
1 32.0 2 1.5万 3
学生活动:学生抢答:
[教法说明]抢答培养学生的竞争意识.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com