
3.如果一个矩形的宽与长的比等于黄金比,称这个矩形为黄金矩形.你能作一个黄金矩形吗?
2.作一条线段的黄金分割点.
如图,已知线段AB,按照如下方法作图:(1)经过点B作BD⊥AB,使BD=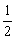 AB.
AB.
(2)连接AD,在DA上截取DE=DB.
(3)在AB上截取AC=AE.则点C为线段AB的黄金分割点.(你知道为什么吗?)
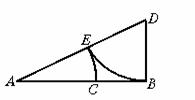
在五角星图案中,大家用刻度尺分别度量线段AC、BC的长度,然后计算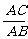 、
、 ,它们的值相等吗?(学生也可利用课本p109上的五角星)
,它们的值相等吗?(学生也可利用课本p109上的五角星)
1.黄金分割的定义
在线段AB上,点C把线段AB分成两条线段AC和BC,如果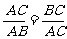 ,那么称线段AB被点C黄金分割(golden section),点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.其中
,那么称线段AB被点C黄金分割(golden section),点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.其中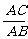 =
=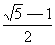 ≈0.618.
≈0.618.
请大家想一想,这个比例式还有其他表示方法吗?
可表示为:AC2=BC×AB.根据这个表达式,你能用自己的语言描述一下黄金分割的定义吗?(突出AC是AB、BC的比例中项)
6.给定一条线段AB,如何找到它的黄金分割点C呢? (1)作BD⊥AB,且使BD= (2)连接AD,以D为圆心,BD长为半径画弧交AD于点E; (3)以A为圆心,AE长为半径画弧交AB于点C. 点C就是线段AB的黄金分割点. 如果有兴趣的话,你可以和同学们探索一下,点C为什么是线段AB的黄金分割点?
[后花园] 妙趣角:耐人寻味的黄金分割 古希腊数学家、天文学家欧多克索斯(Eudoxus)曾提出:能否将一条线段分成不相等的两部分,使较短线段与较长线段的比等于较长线段与原线段的比?这就是黄金分割问题,这个相等的比就是 很长时间里,人们非常崇拜黄金分割.比如,古希腊的许多矩形建筑中,宽与长的比都等于黄金比.有思想的是,优选法中的“0.618法”与黄金分割紧密相关.20世纪70年代,这种方法经著名数学家华罗庚的倡导,在我国得到大规模推广,并取得了很大的成果. 智力操 你想画1个如下图所示的五角星吗?这首先需要画出1个正五边形,然后连接正五边形的所有对角线,就构成1个五角星了!
如何画正五边形呢?可按下面的方法来画: (1)过圆心O作相互垂直的两条直径AC、BD; (2)以OC的中点E为圆心,EB长为半径画弧,交AO于点F; (3)以BF为半径,从圆周上B点起依次截取,就可得到正五边形的5个顶点. 你也试着画画看! 其实想做一个五五边形,有一张纸条就够了,做法很简单.取一张边缘平行的纸条,按图示的方法打一个结,拉紧压平,注意不要起皱纹,再裁去多余的部分,剩下的就是正五边形了.
量量你画的五角星中AF、AG、AC的长度,求出 5.根据人的审美观点,当人的下肢长与身高之比为0.618时,能使人看起来感到匀称.某成年女士身高166cm,下肢长101cm,持上述观点,她所选的高跟鞋的最佳高度约为多少?(精确到0.1cm) 4.如图2,在“黄金矩形”ABCD(即 (1)观察矩形⑤,你认为它也是一个黄金矩形吗? (2)设BC=1(单位长度),通过计算,能否验证你的判断? [拓展与延伸] 3.如图1,在等腰三角形ABC中,AB=AC,∠=36°,BD为∠ABC的平分线,CE是 ∠ACB的平分线,BD、CE相交于点O.图中的黄金三角形有( ). (A)3个 (B)4个 (C)5个 (D)6个
(1) (2) 2.已知M、N是线段AB上的两个黄金分割点.若AB=1cm,则MN≈_______cm. 1.已知C是线段AB的黄金分割点(AC>BC),AC是线段______与线段______的比例中项,如果AB=10cm,那么AC≈_______cm,BC≈_________cm. 2.通过生活中的具体实例,体会黄金分割在生活中的价值,感受黄金分割带来的美. [基础与巩固] 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |